１　内分と外分の公式の導き方

　線分ＡＢをｍ：ｎに内分する点は図のように考えるとよいと思います。

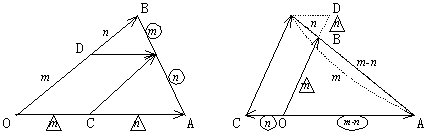
　図から、を得る事ができます。

　教科書にはで考えていますが、ベクトルの和と考えるほうが簡単なように思います。

２　直線，について

　グラフとはある関係を満たす点の集合であるということは、1年生の段階から教えています。直線の式とは、たとえば集合 {(x,y) : y=2x+1} を単に y=2x+1と書くというものだと理解させています。そこで、本来 と書くところをと省略して書いていると教えています。

　また、（sとtの条件） の図形については とすると，

　　p=s(1,0)+t(0,1)=(s,0)+(0,t)=(s,t) ですから，例えば、

　　（2s+3t<6,s>0,t>0）は，Ｐ(x,y)によって直交座標で考えると、

　　{(x,y) : 2x+3y=6 x>0,y>0} になります。

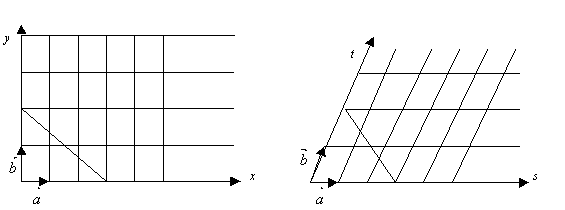
　つまり、ベクトルの点の存在領域の問題を、不等式で表される領域の問題に変更できるのです。

　これは、とした特殊な場合ですが、特殊な場合での答えで十分です。とには何らの制限がないからです。しかし、一般性を求めるならば、このグラフを机の上に張りつけ、斜めから見ると、一般のベクトルになります。この時に、次の性質を考えていればよいのです。

　　　（１） 直線は斜めから見ても直線 （２） 分点の比は変わらない

　一般的には、行列 による一次変換によって、は(p,q)へ、は(r,s)へ変換され斜交座標を考えることになりますが、新課程では、教えてはいません。ここではその説明は省きます。

３　メネラウスの定理

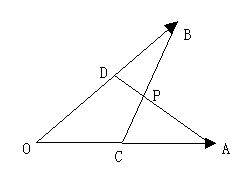　旧課程では裏業であったメネラウスの定理も、新課程ではようやく日の目をみることになりましたが、それでも、平面幾何を履修する高校が少ないので、やはり裏業に終始しています。しかし、このメネラウスの定理というのは、何と覚えにくく、また使いにくい定理なのだろうと思います。それも、平面幾何での図形（三角形に直線を引く）とベクトルでの図形（分点と頂点を結ぶ直線の交点）では構成のイメージが違うからだと思います。、そこで、ベクトルにはベクトルのメネラウスの定理ということで、私は、ベクトルの終点から、

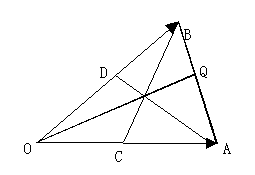　　内分×外分×内分 ＝１ と教えています。

　　　ということになるわけです。

　当然チェバの定理は内分×内分×内分 ＝１ ということになります。

　余談ですが、辺がこのような順に並んでいる参考書をさがしたのですが、ありませんでした。というより、辺の順序が何通りかあって、どれが本物（？）なのか判断しかねます。数学辞典ではアフェイン幾何上の定義があって、これによると、上の式も認められるような気がします。