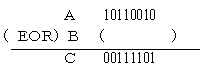等比数列の和の応用問題で複利計算が載せられている教科書が多いが、商業高校においては、「計算事務」という科目で次のような学習をする。
（１）単利の計算
単利法による利息や元利合計は、次の式で求められる。
利息＝元金×利息×期間
元利合計＝元金＋利息
＝元金×（１＋利率×期間）
ここで、
元利合計＝元金×（１＋利率×期間）
について、
＝元金＋（元金×利率×期間）
＝元金＋（１期間後の利息×期間）
となり、元金をａ、１期間後の利息をｄ、期間をｎとするとき、
＝ａ＋ｎｄ（ｎ＝１，２・・・）
で、元金を初項、１期間後の利息を公差、とする等差数列となる。
（注）「１期間後の利息」というのは、私の造語です。
例）元金\2,000,000を年利率4.9％で3ヶ年借りると、期日に支払う元利 合計はいくらか。
解）１年の利息＝\2,000,000×0.049＝\98,000
元金合計＝\2,000,000＋\98,000×3＝\2,294,000
以下のように表にしてまとめていくと、１年の利息である\98,000を順次加えていくことで、n年後の元利合計を求めることが可能になる。
| |
１年後 |
２年後 |
３年後 |
|
ｎ年後 |
| 元 金 |
\2,000,000 |
\2,000,000 |
\2,000,000 |
… |
\2,000,000 |
| 利 息 |
\98,000×1 |
\98,000×2 |
\98,000×3 |
… |
\98,000×n |
| 元利合計 |
\2,098,000 |
\2,196,000 |
\2,294,000 |
… |
\2,000,000＋\98,000n |
ただし、「n年後」となっていることから、教科書に掲載されている等差数列の一般項
aｎ = a + (n－1)d
とは形が異なるので、問題中の表現を工夫して整合性を取る必要があるかもしれないが、銀行の預貯金や車のローンなど、日常生活に見られる数列の例として、現在の低金利やローン地獄など、金融に関する問題の一部を、数学を通してみることができると思われる。
「計算事務」の教科書には、この他に以下のような問題が挙げられている。単位をそろえなければならない場合、nが有理数となる場合など、数列という話題からは離れていくが、商業高校において学習されている内容を紹介する意味で付記しておく。
例題１）元金\600,000を年利率7%で3年間貸し付けると、利息はいくらか。
解）\600,000×0.07×３＝\126,000
例題２）元金\200,000を年利率6.5%で9ヶ月間借りると、期日に支払う元利合計はいくらか。
解）\200,000×（1＋0.065×9/12）＝\209,750
例題３）元金\80,000を年利率5%で1年4ヶ月貸し付けると、利息はいくらか。 （円未満切り捨て）
解）1年4ヶ月＝16ヶ月
\80,000×0.05×16/12＝\5,333
例題４）元金\90,000を年利率9%で2月16日から4月30日まで貸し付けると、利息はいくらか。（平年、片落とし）
解）2/16～4/30………73日
\90,000×0.09×73/365＝\1,620
（２）複利の計算
単利計算を学習した後、複利の計算も学習する。
複利終価及び複利利息を求める式は次のようになる。
複利終価＝元金×（１＋利率）記数
複利利息＝複利終価－元金
＝元金×｛（１＋利率）記数－１）｝
ここで、
複利終価＝元金×（１＋利率）記数
について、元金をａ、（１＋利率）をｒ、期数をｎとするとき、
＝ａｒｎ （ｎ＝１，２・・・）
で、元金を初項、（１＋利率）を公比、とする等比数列となる。
例題１）元金\100,000を年利率6%、1年1期の複利で3年あずけると、複利終価はいくらになるか。（円未満4捨5入）
解）\100,000×（1＋0.06）=\106,000………1期末の合計
\106,000×（1＋0.06）=\112,360………2期末の合計
\112,360×（1＋0.06）=\119,102………3期末の合計
上の式をまとめると、
\100,000×（1＋0.06）×（1＋0.06）×（1＋0.06）
＝\100,000×（1＋0.06）３ ＝\100,000×1.191016 ＝\119,102
単利計算と複利計算で、公差、公比にあたるものが異なることから、２つの利息を求める式には大きな違いがあることがわかる。
例題２）\500,000を年利率7%、1年1期の複利で、5年間借り入れると、複利終価はいくらになるか。（円未満4捨5入）
解）\500,000×（1＋0.07）５ ＝\500,000×1.40255173 ＝\701,276
例題３）\300,000を年利率6%、半年1期の複利で、４年６ヶ月間貸し付けると、複利利息はいくらになるか。（円未満4捨5入）
解）半年1期であるから、6%÷2＝3%………１期の利率
4（年）×2＋1期（6ヶ月）＝9期………期数
\300,000×｛（1＋0.03）９－1｝ ＝\300,000×（1.30477318－1）＝\91,432
そして、複利計算の応用として次のような問題もある。前者は単利と複利計算の融合問題、後者は利息をつける場合の条件付き問題とでもいうものである。
◎端数期間がある場合
貸借期間に、１期に満たない端数が含まれているときには、この端数の部分については単利法で計算する。
例題）元金\400,000を、年利率6%、半年1期の複利で、4年9ヶ月間あずければ、複利終価及び複利利息はいくらになるか。ただし、端数期間は単利法による。（計算の最終で円未満4捨5入）
解）半年1期であるから、6% ÷2 = 3% ………1期の利率
4年×2＋1期（6ヶ月）＝9期………期数
9ヶ月－6ヶ月＝3ヶ月………端数月数
\400,000×（1＋0.03）９
＝\400,000×1.30477318………９期までの複利終価
\400,000×1.30477318×（1＋0.06×3/12）
＝\400,000×1.30477318×1.015＝\529,738
\529,738－\400,000＝\129,738
◎一定金額に利息をつけない場合
利息を計算するときに、一定額以上の金額にだけ利息をつける場合がある。この一定金額を付利単位という。この場合には、１期ずつ複利終価や複利現価を計算することになる。
例題）元金\800,000を、年利率6%、半年1期の複利で、1年6ヶ月間あずければ、複利終価はいくらか。ただし、毎期\100未満の金額には利息をつけないで計算するものとする。
解）付利単位が\100なので、利息計算には、毎期元金の\100未満は含めない。
\800,000×（1＋0.03）＝\824,000………第１期末の元利合計
\824,000×（1＋0.03）＝\848,720………第２期末の元利合計
\848,700×（1＋0.03）＋\20＝\874,181
「プログラミング」というの授業の中で、「基数記数法」について学習する。
（１）10進数
10進数の「254」は、
254＝2×10２＋5×10１＋4×10０
このとき、10を「基数」、基数の整数条を「重み」という。そして、0～9までの10個の数字を使用し、10という基数で位取りすることを「10進法」という。
（２）2進数
コンピュータは、電流が流れているかいないかなどのように、２つの状態しか判断できない。 これを「0」と「1」に対応させて、「2」を基数とする表現方法を「2進法」という。こうすると、データ表現に都合がよい。
（３）16進数
コンピュータが扱う数字は基本的に2進数であるが、使う数字は「0」「1」だけなので、表記すると非常に長くなってわかりづらい。そこで、2進数の4桁分を1桁に表現する16進数を用いると、表記も短くなり、２進法の４桁の１６通りの表現を区別できるために便利である。
そして、この後は「基数変換」といい、例えば、２進数の１０進数への変換を行う。
① 2進数→10進数
（例１）2進数1101を10進数に変換しなさい。
解）(1101)２ ＝1×2３＋1×2２＋0×2１＋1×2０
＝1×8＋1×4＋0×2＋1×1
＝8＋4＋0＋1
＝13
（例２）2進数110.01を10進数に変換しなさい。
解）(110.01)２ ＝1×2２＋1×2１＋0×2０＋0×2－１+1×2－２
＝1×4＋1×2＋0×1＋0×0.5＋1×0.25
＝4＋2＋0＋0＋0.25
＝6.25
② 10進数→2進数
（例１）10進数23を2進数に変換しなさい。
解）10進数を2で順番に割っていき、その商と余りから答を求める。
2 23…1
2 11…1
2 5…1
2 2…0
1
（23）１０＝（10111）２
（例２）10進数0.45を2進数に変換しなさい。
解）10進数を２で順番に掛けていき、整数部分を取り出すことにより、答を求める。
0.45× 2 ＝ 0.9 → 0
0.9 × 2 ＝ 1.8 → 1
0.8 × 2 ＝ 1.6 → 1
0.6 × 2 ＝ 1.2 → 1
0.2 × 2 ＝ 0.4 → 0
0.4 × 2 ＝ 0.8 → 0
0.8 × 2 ＝ 1.6 → 1
0.6 × 2 ＝ 1.2 → 1
0.2 × 2 ＝ 0.4 → 0
（0.45）１０＝（0.011100110…）２
③ 2進数→16進数
（例）2進数1001011を16進数に変換しなさい。
解）右から4桁ずつに分けて、16進数に対応させる。4桁に足らない場合は、左側に0を入れて考える。
100 1011
↓ ↓
0100 1011
↓ ↓
４ Ｂ
（1001011）２＝（4B）１６
④ 16進数→2進数
（例）16進数F4Cを2進数に変換しなさい。
解）16進数を4桁ごとの2進数に対応させる。
F 4 C
↓ ↓ ↓
1111 0100 1100
（F4C）１６＝（111101001100）２
⑤ 16進数→10進数
（例）16進数3A.8を10進数に変換しなさい。
解）基数記数法で表現し、計算する。A～Fは、10～15と置き換える。
（3A.8）１６＝3×16１＋10×16０＋8×16－１
＝48＋10＋0.5＝58.5
⑥ 10進数→16進数
（例）10進数19.75を16進数に変換しなさい。
解）整数部は基数16で割っていき余りを、小数部は16を掛けていき、整数部を求める。
（整数部） （小数部）
16 19…3 0.75×16＝12.0
1
0.0 ＜終＞ C
（19.75）１０＝（13.C）１６
（１）論理演算
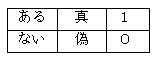左図のように２つの状態のうちどちらか一方の状態をとる場合、そのものがとっている状態を論理値とよぶ。また、与えられた１つ以上の論理値から、新しい論理値を作り出す演算が論理演算と呼ばれる。
ア NOT 与えられた状態の逆の結果を導き出すことをいう。（否定）
（例） 0 → 1
イ OR 同時に与えられた２つ以上の状態のうち、１つ以上が１であれば、結果として１を導き出し、すべてが0であれば0を導き出す働きをいう。（論理和）
（例） 0＋0＋1＋0＋0＋0＋0＋0 → 1
0＋0＋0＋0＋0＋0＋0＋0 → 0
ウ AND 同時に与えられた２つ以上の状態がすべて１のときのみ１と結果として導き出し、0が1つでもあれば0となる。（論理積）
（例） 0×0×1×0×1×1×1×1×1 → 0
1×1×1×1×1×1×1×1×1 → 1
エ EOR 与えられた２つ以上の論理値が同じならば０を、異なっていれば１を結果として導き出す。（論理差、排他的論理和）
（例） １＊１ → ０
１＊０ → １
例題 ビット列Ａとビット列Ｂの排他的論理和（ＥＯＲ）の結果がビット列Ｃとなるとき、ビット列Ｂの値はどれか。
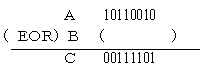
ア 00110000 イ 01110000
ウ 10001111 エ 10111111
（答）ウ
（２）集合
数学Ａ同様に、以下の集合の学習を行う。
・集合と要素 ・部分集合 ・全体集合と補集合 ・ベン図による論理式の表現
例題 ベン図の網掛け部分に対応する論理式として正しいものはどれか。ここで"・"は論理積、"＋"は論理和、ＸはＸの否定を表す。
ア Ａ・Ｂ＋Ｂ・Ｃ イ（Ａ＋Ｂ）・Ｃ ウ Ｂ・（Ａ＋Ｃ） エ Ｂ・（Ａ＋Ｃ）
（答）エ
（３）基本演算回路
先の論理演算を電気回路に導入したのが下図である。
この回路等を用いて、２数の和を作る回路を総称して加算器という。その代表的なものとして、半加算器と全加算器が挙げられる。
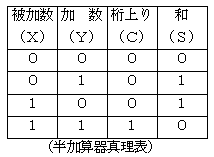
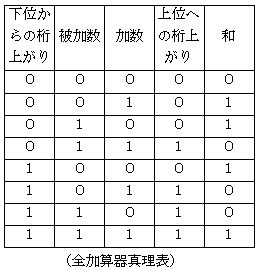
例題 次の図は全加算器を表した論理回路である。図中ｘに１、ｙに０、ｚに１を入力したとき、出力Ｃ（キャリー）、ｓ（和）の値はどうなるか。
ア ｃ＝０、ｓ＝０ イ ｃ＝０、ｓ＝１ ウ ｃ＝１、ｓ＝０ エ ｃ＝１、ｓ＝１ オ ｃ、ｓともに不定
（答）ウ