 杒奀摴峕暿崅摍妛峑丂彫丂嶳丂栁丂庽
杒奀摴峕暿崅摍妛峑丂彫丂嶳丂栁丂庽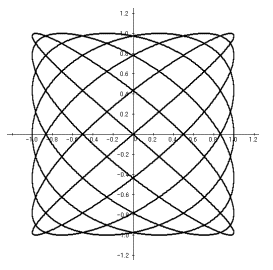
乮戞侽愡乯俥倳値們倲倝倧値丂倁倝倕倵丂偺憖嶌偵偮偄偰
|
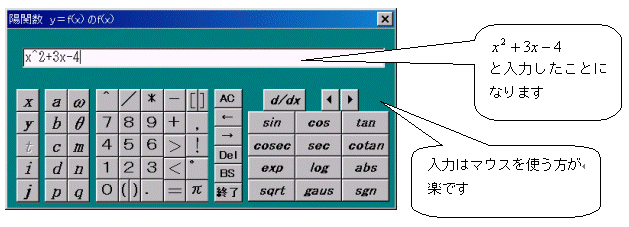
娭悢昞帵僜僼僩乮Function View乯偺巊偄曽
- 乽Function View乿偑婲摦偡傞
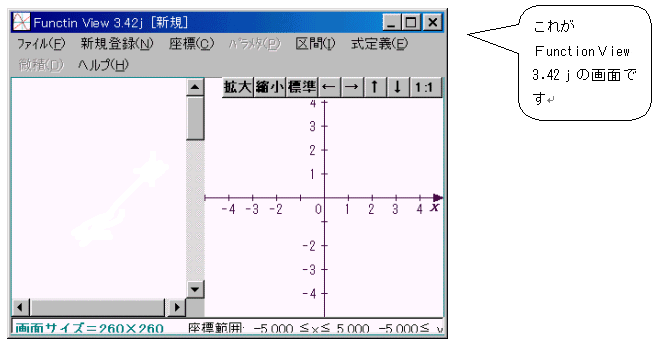
師偺夋柺偼壓恾偺傛偆偵側傝傑偡丅
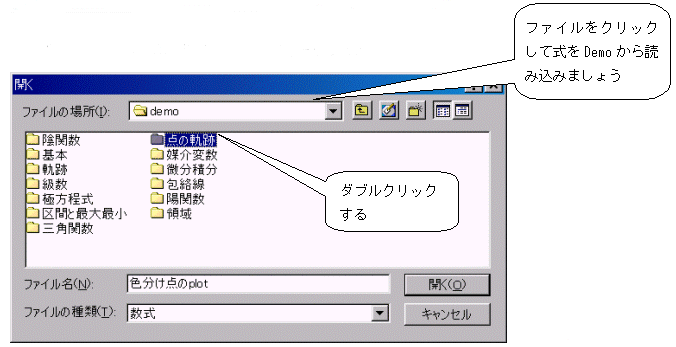
- 乽揰偺婳愓乿偺怓暘偗揰plot傪奐偄偰傒傑偟傚偆
拲堄帠崁
嘆僼儘僢僺乕僨傿僗僋偐傜撉傒崬傓応崌偼丄懡彮帪娫偑偐偐傝傑偡丅
丂僴乕僪僨傿僗僋偵僐僺乕偡傞偙偲傪偍彠傔偟傑偡丅
嘇嫵壢彂偵崌傢偣偨栤戣傪曐懚偱偒傞僼僅儖僟傪嶌偭偰偍偔偲曋棙偩偲巚偄傑偡丅墘廗侾丏倓倕倣倧偐傜奐偄偰傒傑偟傚偆
乮侾乯乽嬫娫偲嵟戝嵟彫僼僅儖僟乿偺拞偵偁傞乽俀師娭悢偺嵟戝抣僼傽僀儖乿傪奐偔
丂丂丂丂丂丂佀嬫娫傪僷儔儊僞偱堏摦偝偣傞
乮俀乯乽嶰妏娭悢僼僅儖僟乿偺拞偵偁傞乽梋尫嬋慄僼傽僀儖乿傪奐偔
丂丂丂丂丂丂佀僷儔儊僞曄峏偱巆憸昞帵偝偣偰梋尫偺僌儔僼傪偐偔
乮俁乯乽梲娭悢僼僅儖僟乿偺拞偵偁傞乽俁師娭悢偲夝俀僼傽僀儖乿傪奐偔
丂丂丂丂丂丂佀僷儔儊僞曄峏偱倃幉偲偺岎揰偺條巕傪挷傋傞
乮係乯乽椞堟僼僅儖僟乿偺拞偵偁傞乽墌偲捈慄偺椞堟僼傽僀儖乿傪奐偔
乮俆乯乽旝暘愊暘僼僅儖僟乿偺拞偵偁傞乽暯嬒曄壔棪僼傽僀儖乿傪奐偔
丂丂丂丂丂丂佀倱倲倎倰倲傪僋儕僢僋偟偰條巕傪傒傞墘廗俀丏怴婯搊榐偟偰僌儔僼傪昞帵偝偣傑偟傚偆
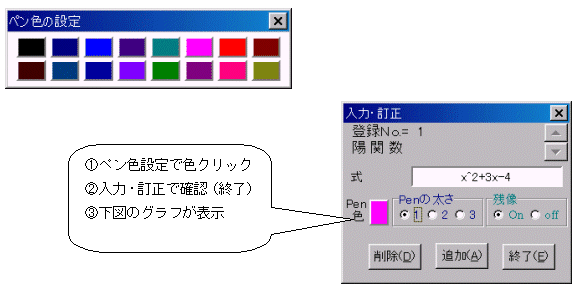
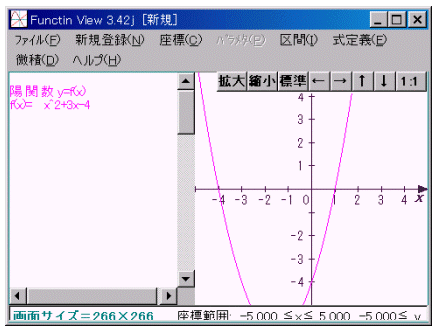 丂仢 娭悢偺捛壛偼丄娭悢幃傪僋儕僢僋乽擖椡丒掶惓乿偱捛壛乮嶍彍乯偱偒傞
丂仢 娭悢偺捛壛偼丄娭悢幃傪僋儕僢僋乽擖椡丒掶惓乿偱捛壛乮嶍彍乯偱偒傞
丂仢 娭悢傗揰摍偼丄侾俇屄傑偱擖椡壜擻乮儁儞怓偑侾俇怓側偺偱乯
丂仢 嵗昗偺奼戝丒弅彫傗堏摦偼塃偺儊僯儏乕偱娙扨偵峴偆偙偲偑偱偒傞
丂仢 嬫娫愝掕偟偰嬫娫偺忋尷偲壓尷傪擖椡偡傟偽丄嵟戝抣丒嵟彫抣偺昞帵傕娙扨偵偱偒傞
丂仢 旝愊偐傜嬫暘媮愊傕偱偒傞偟丄掕愊暘偺寁嶼傕壜擻
丂仢 娭悢偵倎傗倐傪擖椡偟偨応崌偼丄僷儔儊僞曄峏偱傾僯儊乕僔儑儞偑傒傜傟傞
栤戣侾丂2師娭悢倷亖倶俀亄俆倶亅俁乮亅俁亝倶亝侾乯偵偍偗傞嵟戝抣丒嵟彫抣傪媮傔傞丅
丂丂傑偨丄偦偺偲偒偺x偺抣傪媮傔傞丅
僸儞僩丗怴婯搊榐仺梲娭悢偱擖椡丄嵗昗傪弅彫丄嬫娫仺嬫娫愝掕乮壓尷丄忋尷偺弴乯
栤戣俀丂娭悢倷亖乥倶俀亅係倶乥亅倶偺僌儔僼傪偐偔丅
僸儞僩丗怴婯搊榐仺梲娭悢偱擖椡丄愨懳抣偼abs(丂)傪僋儕僢僋
栤戣俁丂娭悢倷亖俀sin倶偺僌儔僼傪偐偔丅
僸儞僩丗怴婯搊榐仺梲娭悢偱擖椡丄惓尫偼sin傪僋儕僢僋丄嵗昗仺斖埻曄峏偱x幉栚惙傪曄峏
栤戣係丂晄摍幃(倶亅俀)俀亄(倷亄侾)俀亞俋偺昞偡椞堟傪恾帵偡傞丅
僸儞僩丗怴婯搊榐仺恾宍幃偱擖椡丄嫬奅慄偺怓偲椞堟偺怓傪僋儕僢僋
栤戣俆丂2捈慄俀倶亄倷亅俇亖侽丆倶亅俁亖侽傪恾帵偡傞丅
僸儞僩丗怴婯搊榐仺堿娭悢偱擖椡丄嵍曈偺擖椡偺傒偱傛偄丄2杮栚偼捛壛傪僋儕僢僋偟偰擖椡
栤戣俇丂暘悢娭悢倷亖(倶俀亄侾)/倶偺僌儔僼傪偐偒丄慟嬤慄偑倷亖倶丆倷亖侾/倶偱偁傞偙偲傪妋偐傔傞丅
僸儞僩丗怴婯搊榐仺梲娭悢偱擖椡丄慟嬤慄偼捛壛傪僋儕僢僋偟偰擖椡
栤戣俈丂墌倶俀亄倷俀亖侾傪攠夘曄悢偱昞帵偡傞丅
僸儞僩丗怴婯搊榐仺攠夘曄悢偱擖椡丄曄悢暥帤偼t偲偡傞丄斖埻偺壓尷偼0丒忋尷偼2兾偲擖椡
栤戣俉丂暋慺悢z偑丄摍幃乥倸亅(俀亄俁倝)乥亖侾傪枮偨偡偲偒偺恾宍傪偐偔丅
丂丂丂乮墳梡偲偟偰丄0亝arg z亝兾偲偟偰傒傞乯
僸儞僩丗怴婯搊榐仺嬌曽掱幃偱擖椡丄r亖1丄拞怱(2丆3)偲偡傞丄斖埻偺壓尷偼0丒忋尷偼2兾偲擖椡
栤戣俋丂懳悢娭悢倷亖倢倧倗俀倶偲倷亖倢倧倗1/2倶偺僌儔僼傪偐偔丅
僸儞僩丗怴婯搊榐仺梲娭悢偱擖椡丄2杮栚偼捛壛傪僋儕僢僋偟偰擖椡
栤戣侾侽丂娭悢倷亖倶(倶亅俀)俀偺僌儔僼傪偐偒丄x幉偲嬋慄偱埻傑傟偨晹暘偺柺愊傪媮傔傞丅
僸儞僩丗怴婯搊榐仺梲娭悢偱擖椡丄旝愊仺掕愊暘丒婎杮掕棟偱嬫娫偺壓尷傪0丒忋尷傪2偲擖椡
栤戣侾侾丂2師娭悢倷亖亅倶俀亄倎倶亅俁乮亅侾亝倶亝俀乯偵偍偗傞嵟戝抣偲嵟彫抣傪媮傔傞丅
僸儞僩丗怴婯搊榐仺梲娭悢偱擖椡丄嬫娫仺嬫娫愝掕乮壓尷丄忋尷偺弴乯丄僷儔儊僞仺a傪0.05昤夋
栤戣侾俀丂俀師晄摍幃倶俀亅倎倶亄俀倎亅俁亜侽偺夝偑偡傋偰偺悢偱偁傞傛偆偵丄掕悢倎偺抣偺斖埻傪媮傔傞丅
僸儞僩丗怴婯搊榐仺梲娭悢偱擖椡丄僷儔儊僞仺倎傪0.05昤夋丒倎亖2乣倎亖6偺偲偒巆憸僠僃僢僋
栤戣侾俁丂嶰妏娭悢倷亖sin倶偺僌儔僼傪傕偲偵偟偰丄學悢偺堄枴傪峫偊傞丅
丂丂丂乮侾乯倷亖倎sin倶
丂丂丂乮俀乯倷亖sin(倶亅兤)
丂丂丂乮俁乯倷亖sin倐倶
僸儞僩丗怴婯搊榐仺梲娭悢偱擖椡丄僷儔儊僞仺倎丄倐傪0.05昤夋丒兤傪昤夋乮1偮偢偮傒傞乯
栤戣侾係丂墌倶俀亄倷俀亖侾俉偲捈慄倷亖倶亄倎偲偺嫟桳揰偺屄悢傪挷傋傞丅
僸儞僩丗怴婯搊榐仺堿娭悢偱墌傪擖椡丒梲娭悢偱捈慄傪擖椡丄僷儔儊僞仺倎傪0.05昤夋
栤戣侾俆丂娭悢倷亖倶俁亅俀倶亅俁偺揰(亅侾丆亅俀)偵偍偗傞旝暘學悢偺堄枴傪峫偊傞丅
丂丂丂乮暯嬒曄壔棪偲愙慄偺孹偒偺峫偊曽傪傒傜傟傞乯
僸儞僩丗怴婯搊榐仺梲娭悢偱擖椡丄旝愊仺暯嬒曄壔棪偱倱倲倎倰倲傪僋儕僢僋
栤戣侾俇丂揰俙(俇丆侽)偲墌倶俀亄倷俀亖侾俇忋偺摦揰俻傪寢傇慄暘俙俻偺拞揰俹偺婳愓傪昞帵偡傞丅
僸儞僩丗幃掕媊偱墌傪擖椡乮掕媊掕悢Q1偲偟偰4cos兤丄Q2偲偟偰4sin兤乯
丂丂丂丂怴婯搊榐仺嬌曽掱幃r=4丄拞怱(0丆0)丄0亝兤亝2兾
丂丂丂丂捛壛偱揰(6丆0)偲揰(Q1丆Q2)
丂丂丂丂偝傜偵捛壛偱揰(6亄Q1)/2丆Q2/2)
丂丂丂丂偝傜偵捛壛偱慄暘(6丆0)偲(Q1丆Q2)丂丂僷儔儊僞仺婳愓僠僃僢僋
栤戣侾俈丂曽掱幃乥倶俀亅俀倶乥亅倎亖侽偺夝偺屄悢偑倎偺抣偵傛偭偰偳偺傛偆偵曄傢傞偐挷傋傞丅
僸儞僩丗怴婯搊榐仺梲娭悢偱擖椡丄僷儔儊僞仺倎傪0.05昤夋
丂丂丂丂傑偨偼丄2偮偺梲娭悢傪擖椡偟偰丄僷儔儊僞
栤戣侾俉丂2師娭悢倷亖倶俀亅俇倶亄俀乮倎亝倶亝倎亄侾乯偵偍偗傞嵟彫抣乮嵟戝抣乯傪昞偡僌儔僼傪昞帵偡傞丅
僸儞僩丗幃掕媊仺娭悢偲掕悢偱擖椡丄掕悢偼俵倝値倁乮乵壓尷丄忋尷乶掕媊娭悢乯
丂丂丂丂捛壛偱丄梲娭悢F1偲揰(倎丆Q1)丄僷儔儊僞偱婳愓僠僃僢僋丄嬫娫愝掕偡傞
栤戣侾俋丂2師娭悢倷亖倶俀亅倶亅俀偵偍偄偰丄倷亜侽偲倷亖侽偲倷亙侽偺奺応崌偺揰傪怓暘偗偟偰昞帵偡傞丅
僸儞僩丗幃掕媊仺娭悢傪擖椡丄捛壛仺揰傪3僷僞乕儞偱擖椡乮F1(倶)亜0偺傛偆偵擖椡乯
栤戣俀侽丂晄摍幃sin兤亝侾/併俀傪枮偨偡揰傪怓暘偗偟偰昞帵偡傞丅
僸儞僩丗幃掕媊仺娭悢傪2偮擖椡丄捛壛仺梲娭悢2偮偲揰傪擖椡
栤戣俀侾丂俀捈慄倶亅倷亅侾亖侽偲倶亄俀倷亅係亖侽偺岎揰傪捠傝丄揰(俁丆亅侾)傪捠傞捈慄傪媮傔傞丅
僸儞僩丗怴婯搊榐仺堿娭悢傪3偮擖椡丄捛壛仺揰偱岎揰偲梌揰傪擖椡丄僷儔儊僞偱昤夋
栤戣俀俀丂倶丆倷偑係偮偺晄摍幃倶亞侽丆倷亞侽丆俀倶亄俁倷亝侾俀丆俀倶亄倷亝俉傪枮偨偡偲偒丄倶亄倷偺嵟戝抣偲嵟彫抣傪媮傔傞丅
僸儞僩丗怴婯搊榐仺恾宍幃偱乮丂乯偵堦偮偢偮擖椡偟偰丄4偮偺乮丂乯傪暲傋傞丄捛壛仺堿娭悢
乮戞係愡乯嫵壢彂椺戣丒楙廗乮悢尋弌斉怴曇悢妛嘦戞侾復恾宍偲曽掱幃乯
|
椺俀乮侾係儁乕僕乯
俀揰 俙(亅俀丆俆)丆俛(係丆亅侾) 傪寢傇慄暘俙俛偑偁傞丅慄暘俙俛傪俀丗侾偺斾偵撪暘偡傞揰偺嵗昗傪媮傔傛丅傑偨丄慄暘俙俛傪俀丗侾偺斾偵奜暘偡傞揰 偺嵗昗傪媮傔傛丅椺俈乮俀俀儁乕僕乯
俀捈慄倶亅倷亅侾亖侽丆倶亄俀倷亅係亖侽偺岎揰偲揰(俁丆亅侾)偲傪捠傞捈慄偺曽掱幃傪媮傔傛丅楙廗侾俇乮俀俁儁乕僕乯俀捈慄倶亄俀倷亅俁亖侽丆倶亅俀倷亄俀亖侽偺岎揰偲揰(亅俁丆侽)偲傪捠傞捈慄偺曽掱幃傪媮傔傛丅椺侾係乮俁俉儁乕僕乯俀揰A(侽丆侽)丆俛(俁丆侽)偐傜偺嫍棧偺斾偑俀丗侾偺斾偵撪暘偡傞揰俹偺婳愓傪媮傔傛丅楙廗俀俈乮俁俉儁乕僕乯俀揰俙(亅侾丆侽)丆俛(俀丆侽)偐傜偺嫍棧偺斾偑侾丗俀偺斾偵撪暘偡傞揰俹偺婳愓傪媮傔傛丅椺戣俈乮俁俋儁乕僕乯揰俙(俇丆侽)偲墌倶俀亄倷俀亖侾俇忋偺揰俻偲傪寢傇慄暘俙俻偺拞揰傪俹偲偡傞丅俻偑偙偺墌忋傪摦偔偲偒丄揰俹偺婳愓傪媮傔傛丅楙廗俀俉乮俁俋儁乕僕乯捈慄俀倶亄倷亄侾亖侽偲揰俙(俁丆侾)偑偁傞丅揰俻偑偙偺捈慄忋傪摦偔偲偒丄慄暘俙俻傪俀丗侾偺斾偵撪暘偡傞揰俹偺婳愓傪媮傔傛丅







