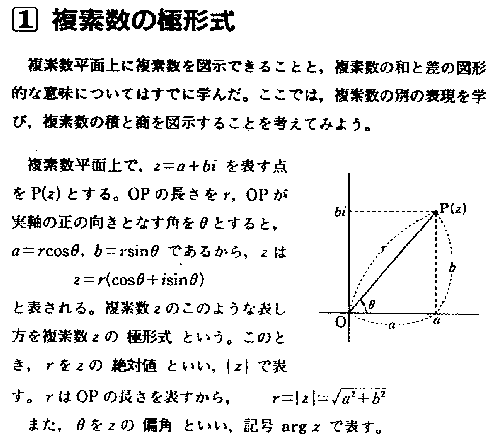
右のような説明から始めると、極形式を学ぶ意義が生徒に伝わらないばかりか、授業そのものをつまらなくしてしまうと感じ、次のような授業をしてみた。

教科書（第一学習社）のグラビアを見ながら「複素数の積によって描かれるうずまき線について、どのうような規則があるのか調べてみよう！」と投げかけた。

計算し易いように (1+i)の累乗を選び、生徒達は計算結果を複素数平面上に図示していった。

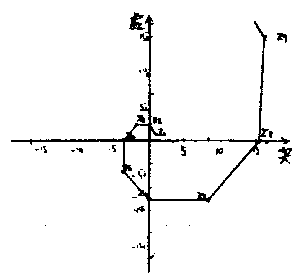
うずまき線になっていることを確認しいよいよ規則探しに入った。
何に注目して規則を探すかとの問いに、「角度、線の長さ」と答えてきたので、「偏角、絶対値」という用語を導入し表にまとめた。

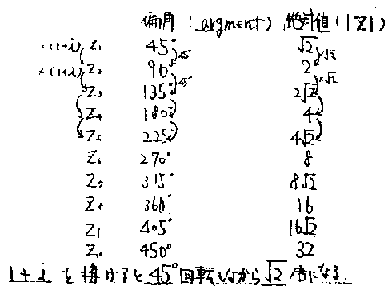
表から、このうずまき線は４５どずつ回転しながら、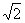倍になっていることが容易にわかった。
　そこで、「このような表を作らなくても、1+i を掛けると４５度回転しながら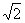倍になることがパッとわかるテクニックを知りたくないかい？」と投げかけた。

このようにして極形式を導入し、複素数を極形式で表すと偏角や絶対値が簡単に求められることを強調し、教科書の練習問題に入っていった。

生徒たちは、導入段階で複素数の積の図形的意味（うずまき線）を経験しているので、この後の学習でわからなくなったときはここへ戻ってきてイメージを思い出すことが可能となった。また、このイメージを基に複素数の商、ド・モアブルの定理などの理解もスムーズにできたと考える。
　三省堂の教科書に右のような例題があるのを後から知った。導入としてまたは練習問題として使用できそうだ。