| 数列の和 | イメージ | 計算式 | 一般化 | |||
|---|---|---|---|---|---|---|
| 1+2+3+4+5 | → | (①) | → | C | → | 1+2+3+…+n=(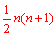 ) ) |
| 12+22+32+42+52 | → | (③) | → | B | → | 12+22+32+…+n2=(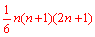 ) ) |
| 13+23+33+43+53 | → | (②) | → | A | → | 13+23+33+…+n3=(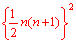 ) ) |
教科書では恒等式を用いる方法が一般的なようですが,「自然数の平方の和」を計算しているという実感に乏しく,生徒には決して一般的とは言えないのではないかと感じていました。今回,「数列の和のイメージ→計算式→一般化」という流れで指導してみたところ,なかなか好評でしたので授業の様子を紹介致します。イメージ選択肢の図は「明解 数学Ⅱ・数学A(三省堂)」からの引用です。
いろいろな数列の和(P.70)
次の数列の和について,そのイメージ・計算式をそれぞれ選択し,一般化してみよう。
| 数列の和 | イメージ | 計算式 | 一般化 | |||
|---|---|---|---|---|---|---|
| 1+2+3+4+5 | → | (①) | → | C | → | 1+2+3+…+n=(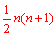 ) ) |
| 12+22+32+42+52 | → | (③) | → | B | → | 12+22+32+…+n2=(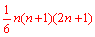 ) ) |
| 13+23+33+43+53 | → | (②) | → | A | → | 13+23+33+…+n3=(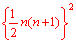 ) ) |
| イメージ選択肢 | 計算式選択肢 | ||
|---|---|---|---|
| ① | 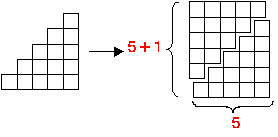 | (A) | (1+2+3+4+5)2 →(1+2+3+…+5)2 → 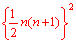 |
| ② | 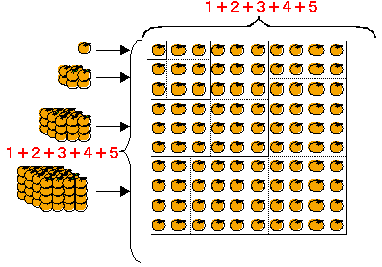 | (B) | 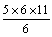 → 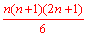 → 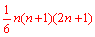 |
| ③ | 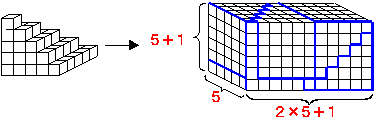 | (C) | 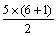 → 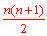 → 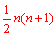 |
| T: | 次の数列の和について,そのイメージと計算式をそれぞれ選択し,一般化してみよう。 |
| T: | 最初の和は1年生のとき習いましたね。イメージと計算式を答えてください。 |
| S: | イメージが①で,計算式は(C)です。 |
| T: | そうですね。これは,「自然数の和」と言って等差数列ですから,階段のイメージでした。等差数列の和は逆さまにして2つ合わせると長方形になるので,(C)のように計算できるのでした。 |
| T: | それでは,一般化してみましょう。この階段が6段,7段と増えつづけ,n段になったとき計算式(C)はどうなると思いますか。 |
| S: | 5がnになるになる |
| T: | そうですね。これはあくまで予想ですが,まず間違いないでしょう。厳密な証明はこの後,数学的帰納法という証明法を用いて勉強しますのでそのときやることにします。 |
| T: | では次に,三番目の数列の和についてイメージと計算式を答えてください。 |
| S: | イメージが②で,計算式は(A)だと思います。 |
| T: | これを「自然数の立方の和」と言います。立方というのは3乗のことですね。体積の単位にも立方が使われていますね。各項のイメージはみかんを縦・横・高さ,すべて同じ個数だけ積んだ立体ですが,和を計算するときはこのように並び替えます。この正方形の一辺の長さはどのようになっていますか。 |
| S: | 「自然数の和」です。 |
| T: | これで計算式が(A)であることがすぐにわかりますね。では,一般化してください。 |
| S: | 5をnにする。 |
| T: | かっこの中は「自然数の和」でしたから,最初に一般化した結果を代入しておくことにしましょう。「自然数の和」と「自然数の立方の和」は非常によく似ているので覚えやすそうですね。 |
| T: | さて,最後に二番目の数列の和について考えてみましょう。これを「自然数の平方の和」と言いますが,③のような階段状に積まれたブロックをイメージしてみます(実際に模型を示す)。これまで同様,計算しやすいように平面状に敷き詰めてみますが上手くいきません。そこで,立体のまま考えることにして,同じブロックのかたまりを6個組み合わせてみます。すると,ピッタリ一致してこのような直方体ができるのです。誰か挑戦してみませんか? |
| S: | あれ,上手くいかないな。(しばらくして)できました。 |
| T: | 計算式は(B)でいいですか。 |
| S: | はい。 |
| T: | では,一般化してください。分子はどうですか。 |
| S: | 5をn,6をn+1,11を2n+1にします。分母は6のままです。 |
| T: | これまでの2つとは,ずいぶん違う結果になりました。「平方の和」と「立方の和」は間違えやすいので,イメージからしっかり理解しておきましょう。 |