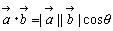 (①)で定義されますが,戸惑う生徒が多く結果的に暗記を強いることになった経験はないでしょうか。さらに,そのあとで成分を用いた定義
(①)で定義されますが,戸惑う生徒が多く結果的に暗記を強いることになった経験はないでしょうか。さらに,そのあとで成分を用いた定義 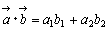 (②)が出てきますが,両者のつながりが見えずらく生徒をますます混乱させているように感じます。ここでは,生徒に無理なく受け入れられ,両者のつながりがよくわかるようにするために②から導入することを提案したいと思います。
(②)が出てきますが,両者のつながりが見えずらく生徒をますます混乱させているように感じます。ここでは,生徒に無理なく受け入れられ,両者のつながりがよくわかるようにするために②から導入することを提案したいと思います。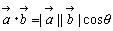 (①)で定義されますが,戸惑う生徒が多く結果的に暗記を強いることになった経験はないでしょうか。さらに,そのあとで成分を用いた定義
(①)で定義されますが,戸惑う生徒が多く結果的に暗記を強いることになった経験はないでしょうか。さらに,そのあとで成分を用いた定義 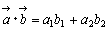 (②)が出てきますが,両者のつながりが見えずらく生徒をますます混乱させているように感じます。ここでは,生徒に無理なく受け入れられ,両者のつながりがよくわかるようにするために②から導入することを提案したいと思います。
(②)が出てきますが,両者のつながりが見えずらく生徒をますます混乱させているように感じます。ここでは,生徒に無理なく受け入れられ,両者のつながりがよくわかるようにするために②から導入することを提案したいと思います。
2.授業例
ボーナスを貰ったS先生は,家族を連れて一皿120円と220円の2種類を扱っている回転寿司に行きました。おなかの膨れた子供たちが,高く積まれた皿の枚数を数えて見ると120円の皿が15枚,220円の皿が11枚ありました。合計金額はいくらになりますか。120×15+220×11=4,220(円)ですね。このことを数学では, 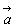 =(120,220) ……値段ベクトル =(120,220) ……値段ベクトル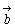 =(15,11) ……個数ベクトル =(15,11) ……個数ベクトル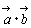 =120×15+220×11=4220 =120×15+220×11=4220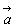 =(a1,a2), =(a1,a2),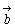 =(b1,b2) のとき =(b1,b2) のとき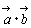 =a1× b1+ a2× b2 =a1× b1+ a2× b2 |
このあと,②から①を導きます。
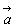 = =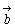 とすると②は とすると②は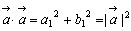 となりますね。これは等しいベクトルの性質です。また, となりますね。これは等しいベクトルの性質です。また,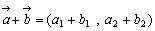 ですから,同様に ですから,同様に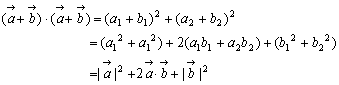 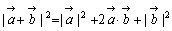 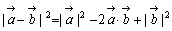 ……(*) ……(*)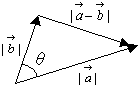 もわかります。ところで右の図において余弦定理より, もわかります。ところで右の図において余弦定理より,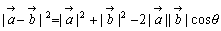 ……(**) ……(**)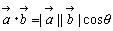 |
3.終わりに