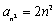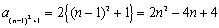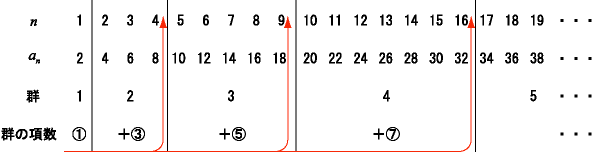
「群の項数」のn個の項の和は,第n郡までの項数,即ち最後の項の番号になっている。
即ち,
| 第2群の最後の項は | 1+3=4 番目 |
| 第3群の最後の項は | 1+3+5=9 番目 |
| 第4群の最後の項は | 1+3+5+7=16 番目 |
| ・・・・・・ | |
群数列が難しいのは,4種類の数字の流れを把握しきれないからである。次のように考えると分かりやすいと思う。
【例】
|2|4,6,8|10,12,14,16,18|20,22,24,26,28,30,32|34,36,・・・
このとき,第n群の最後の項と最初の項を求めよ。
【考え方】

「群の項数」のn個の項の和は,第n郡までの項数,即ち最後の項の番号になっている。
即ち,
| 第2群の最後の項は | 1+3=4 番目 |
| 第3群の最後の項は | 1+3+5=9 番目 |
| 第4群の最後の項は | 1+3+5+7=16 番目 |
| ・・・・・・ | |
【解】