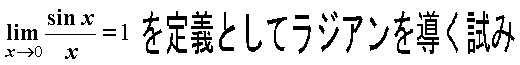
〜微分係数から始まる初等関数の微分法〜
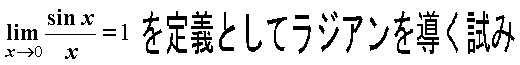
〜微分係数から始まる初等関数の微分法〜
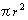 は定義である。よって,さらにラジアンを定義すると,円の面積との組み合わせから,扇形の面積
は定義である。よって,さらにラジアンを定義すると,円の面積との組み合わせから,扇形の面積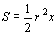 が求められる(∵
が求められる(∵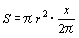 )。数学Ⅲの教科書では,まずラジアンの定義を利用して扇形の面積を求め,それを利用して
)。数学Ⅲの教科書では,まずラジアンの定義を利用して扇形の面積を求め,それを利用して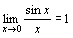 を証明している。これが高校生に指導するこの極限の普通の証明方法である。
を証明している。これが高校生に指導するこの極限の普通の証明方法である。ところが,微分の基礎となる極限の段階で面積という積分を匂わせる道具を使うのは順序が逆のようで何とも気持ち悪い。他の極限と違ってこの極限だけなぜ面積を使わなければ証明できないのか不自然である。自分は高校時代から21年間ずっとこのことを疑問に思い続けながらすっきりしないできた。
このことに関しては,循環論法であるという議論もときどき見かける(例:数研通信平成2年5月号p6〜7「円の面積について」大木実)。しかし,それらを見てもどこかすっきりしないのは,直感的に納得できるものではないからであった。
今年度(11年度)数学Ⅲを担当して,またそのことを思い出した。授業ではいつもの通り証明したが,ずっと気になって頭の中で考えていた。
そして,この極限を利用して,いよいよ三角関数の微分の公式を証明するという授業の日の早朝,「この極限が定義だったらどうなんだろう?」と思いついた。つまり,原点でサインのグラフの接線の傾きが1になるような角の測り方を定義するのである(詳細は後述)。これは「微分係数とは接線の傾きである」という当たり前の発想から「微分係数が簡単な値になるようにできないだろうか」という,指数関数におけるNapierの数の発想と一致するものである(これも詳細は後述)。
21年ぶりの解決に,うれしくて早朝からプリントを作ってその日の授業で生徒に配り,概要を話した。普段からおとなしい生徒たちの反応はいつものように鈍かった。が,後日アンケートをとってみたら35人中5人が「この考え方はおもしろい」と答えてくれた。7人に1人という割合である。これはうまくいった方だ,予想以上によい感触だとうれしく思った。
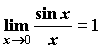 ありき」
ありき」 昔の人が微分係数を発見したとき,2次関数や3次関数など,xのn次式でできる関数のグラフの接線の傾きは簡単な値で結果が求められ,非常に重宝したであろう。最初は今の微分法で使うhを具体的な数値で計算し,徐々にその数値を0に近づけることで推定したが,limitの計算を発見してからはそれで求めたと思われる。ところが,度数法による三角関数のグラフの接線の傾きでは,limitでは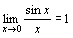 の計算ができないという問題が生じる。よって具体的な数値でしか計算できないが,それで求めても値が非常に小さく,しかも問題なのはその微分係数が非常に中途半端な値だということである。また,指数関数や対数関数も同様に,「計算ができない」「値が中途半端」という問題が生じた。
の計算ができないという問題が生じる。よって具体的な数値でしか計算できないが,それで求めても値が非常に小さく,しかも問題なのはその微分係数が非常に中途半端な値だということである。また,指数関数や対数関数も同様に,「計算ができない」「値が中途半端」という問題が生じた。
そこで昔の人たちは考えた。「三角関数で,微分係数が簡単になるような角度の単位は作れないだろうか」「指数・対数関数で微分係数が簡単になるような底は作れないだろうか」と。そこからラジアンを定義し,Napierの数を発見した。
このように,ラジアンやNapierの数に関しては順序として微分係数が先で,ラジアンという角の単位の定義や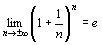 は後だと考えたほうが,教科書の順序よりも自然だと思われる。つまり,はじめに
は後だと考えたほうが,教科書の順序よりも自然だと思われる。つまり,はじめに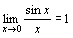 や
や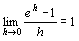 が定義として存在し,そこからπラジアンは180°だとか,eは2.718…だとかが導かれるほうが納得できるということである。
が定義として存在し,そこからπラジアンは180°だとか,eは2.718…だとかが導かれるほうが納得できるということである。
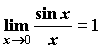 を定義としてラジアンを導く
を定義としてラジアンを導く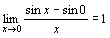 ∴
∴ 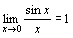
次に,xはどのような角か求める。そのために扇形の面積でX°とxを比較してみる。
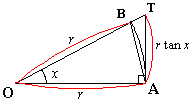 X°=xとし,扇形の面積をSとする。
X°=xとし,扇形の面積をSとする。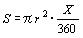 …①であるが,xを用いたときは仮に
…①であるが,xを用いたときは仮に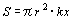 …② としておき,kを求めることにする。角は鋭角として差し支えない。右図において△OAB<S<△OATが成立するから
…② としておき,kを求めることにする。角は鋭角として差し支えない。右図において△OAB<S<△OATが成立するから
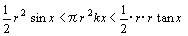
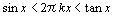
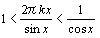
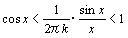
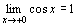 だから,はさみうちの原理より
だから,はさみうちの原理より
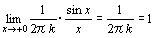 ∴
∴ 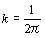
よって①②より
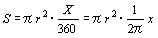 ∴
∴ 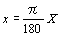
この式よりxの単位はラジアンといえるのだ。
また,y=sin X°の原点における接線の傾きは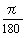 であることも分かる。これを計算すると約0.01745329であるから,この証明の1行目の値と一致する。
であることも分かる。これを計算すると約0.01745329であるから,この証明の1行目の値と一致する。
さらに,②に求めたkの値を代入すると
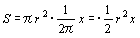
よって,扇形の面積の公式も導かれる。
このことはよく言われることなので敢えてここでとりあげなくてもよいとも思った。しかし,前述の三角関数の場合同様,発想的に自然な感じがして,かつ教科書とは異なるアプローチなのでここで一緒に述べる。
実は授業では,常々数学Ⅱの極限の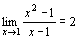 は,2次関数y=x2のx=1における接線の傾きが2になる説明として重要だが,極限の計算としては見え透いたところがあって生徒に説明していても今一つ説得力に欠ける部分が気になっていた。数学Ⅱだから仕方がないといえばそれまでである。しかし,極限の計算として,指数関数y=2xならx=0における接線の傾きは
は,2次関数y=x2のx=1における接線の傾きが2になる説明として重要だが,極限の計算としては見え透いたところがあって生徒に説明していても今一つ説得力に欠ける部分が気になっていた。数学Ⅱだから仕方がないといえばそれまでである。しかし,極限の計算として,指数関数y=2xならx=0における接線の傾きは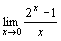 という計算にぶつかると,これは数学Ⅱでは計算できない。このことを2年次に授業では問題提起している。そうしないと極限の計算に問題意識が芽生えないからである。
という計算にぶつかると,これは数学Ⅱでは計算できない。このことを2年次に授業では問題提起している。そうしないと極限の計算に問題意識が芽生えないからである。
さて,今年は数学Ⅲの授業では教科書のように急に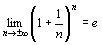 から入ることはしていない。しかし,x=0における接線の傾きが1になるような指数関数の底は2から3の間の数であることは説明した。この程度の大きさであることは生徒には感覚的に示せば,詳細な証明は不要であろうと考え,前述の三角関数の表ではないが,具体的にy=2xなら傾きは約0.69で1より小さく,y=3xなら1.10で1より大きいことを話した。同様にy=log2xのx=1における接線の傾きは約1.44,y=log3xなら約0.91であることも。そしてNapierの数を定義するのであるが,以下の式はみな同値であるという話から始めた。
から入ることはしていない。しかし,x=0における接線の傾きが1になるような指数関数の底は2から3の間の数であることは説明した。この程度の大きさであることは生徒には感覚的に示せば,詳細な証明は不要であろうと考え,前述の三角関数の表ではないが,具体的にy=2xなら傾きは約0.69で1より小さく,y=3xなら1.10で1より大きいことを話した。同様にy=log2xのx=1における接線の傾きは約1.44,y=log3xなら約0.91であることも。そしてNapierの数を定義するのであるが,以下の式はみな同値であるという話から始めた。
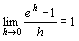 …①
…① 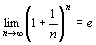 …②
…② 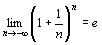 …③
…③
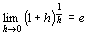 …④
…④ 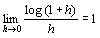 …⑤
…⑤
つまり,いずれを定義としても他の4つは導けるということを以下のように証明するのである。
①から⑤を示す。
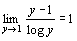 ∴
∴ 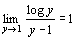
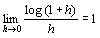
⑤から④を示す。
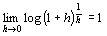 ∴
∴ 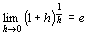
さらに②と③を示す。
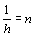 とおくと
とおくと 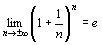
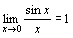 」は同値であり,自分の疑問は,「自然な流れで数学というものを『納得したかった』」ということにあったと思う。
」は同値であり,自分の疑問は,「自然な流れで数学というものを『納得したかった』」ということにあったと思う。生徒は普段,程度の差はあれ「どうして? なぜ?」といつも考えている。だから授業中もそういう点はとことん説明をしているつもりである。例えば,なぜ角度を急にラジアンにするのかという生徒の疑問に対しては,ラジアンにするとsinの微分がcosになって楽だからと説明していた。この説明で納得する生徒ばかりではにのではないか? 即ち,タイトルにある疑問を持ってしまうとこれでは説明にならない。
かといって現実にはこのままラジアンを定義したらかえって難しくて生徒には分からなくなるから無理である。しかし,誰かはまた持つであろうこの疑問の解決のために,今後も数学Ⅲを教えるときにはこの内容のプリントを配ろうと思っている。
参考文献:数研通信 平成2年5月号p6〜7「円の面積について」大木実