

| 数学Ⅱ | |
| 数件出版 新編数学Ⅱ | |
| 数件出版 エディノート数学Ⅱ | |
| 第3章 指数関数と対数関数 5.対数関数とそのグラフ | |
| 1単位時間(1単位時間50分) | |
| 別紙プリント1枚 ムービル数学Ⅱ、N88BASICで作成したソフト | |
| ・「ムービル数学Ⅱ」 河合塾 24 LOG箱 25 逆関数のグラフと指数・対数 ・数学教室「指数・対数関数」N88BASIC 夕張緑ケ丘実業高校 本間比呂志先生作成 | |
| パーソナルコンピュータ CPU 80286以上 メモリ 1.6Mバイト以上 ハードディスク 必要なし |
![]() はじ め に(教材について)
はじ め に(教材について)
![]()
これまで、指数関数のグラフ,対数関数のグラフは、あまり時間を割いて指導してこなかった。指数や対数自体について理解がおぼつかないため、時間をかけてちゃんと点を取ってグラフを書かせても、なかなか定着が悪かった。また、2次関数のグラフのように、いろいろなところで再び登場するわけでもないので、ついついおざなりの指導になり、指数不等式や対数不等式を解くときにも、
| 底が1より大きいときは、不等号の向きは変わらない。 底が1より小さいときは、不等号の向きが逆になる。 |
と半ば機械的に指導してきた。
厚別高校での最初の対数の指導で驚いたことは、対数の定義を時間をかけ丁寧に指導したにもかかわらず、毎時間、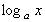
そこで、対数関数のグラフで実際に底が変化するとグラフの形がどのように変化するかを見せることにより、「底」「真数」についてその存在と違いをアピールするとともに、
・指数関数のグラフと対数関数のグラフの位置関係
・グラフの漸近線
・グラフが必ず通る点
といった事項について、イメージをしっかり持たせたいと考え、コンピューターを使ったプリント授業により指導してみる事にした。
![]() 対数関数のグラフの指導について
対数関数のグラフの指導について
![]()
1.本 時 の 目 標
対数関数のグラフについては、
(1)対数関数 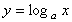
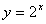
さらにコンピューターで②のグラフが ①のグラフに移動する様子を見せるこ とにより定着を図る。
(2)底の値と対数関数のグラフの形の関係を理解し、対数関数のグラフについてしっかりイメージが持てるようにする。
また、これだけではちょっと時間があまりそうだったので、定着の悪かった対数計算を、を利用して、ゲーム感覚で楽しくやってみることとし、(1),(2)と直接は関係ないが
(3)対数の値を求める計算に習熟させる。
を3つ目の目標とした。
2.学 習 指 導 案
| 指導教諭 | 札幌厚別高等学校 川崎 義明 | ||||||
|---|---|---|---|---|---|---|---|
| 教科 | 数学 | 科目 | 数学Ⅱ | 学年・組 | 2年5組 男子18名 女子22名 計40名 | ||
| 日時 | 平成8年11月19日(火) | 使用教室 | 1階 情報処理教室 | ||||
| 教科書補助教材 | 高等学校 新編 数学Ⅱ(数件出版) エディノート数学Ⅱ(数件出版) | 小単元名 | 5.対数関数とそのグラフ | ||||
| 単元名(配当時間) | 第3章 指数関数と対数関数 (20時間) | 本時の位置 | 1時間目/4時間 | ||||
| 本時の目標 | ・対数関数のグラフの特徴を理解し、具体的な対数関数のグラフを掛けるようにする。 ・対数の値の求め方の練習を行い定着させる。 | ||||||
| 段階 | 学習内容 | 形態 | 教師の活動 | 指導上の留意点 | ||
|---|---|---|---|---|---|---|
| 認知・技能 | 情意 | |||||
| 導入 5分 | 導入 | 既習内容の復習 | 一斉 | ・入室してくる生徒に、プリントとフロッピィを渡し、準備させる。 ・生徒の座席、出欠の確認。 ・指数関数の定義、グラフの特徴を発問して復習する。 | 底による形の違いやグラフが必ず通る点、漸近線について特に注意する。 | 生徒の健康状態、教室の環境等を把握する。 明るい雰囲気作りを心がける。 |
| 課題設定 | ①対数関数とはどのような関数か。 ②指数関数のグラフと対数関数のグラフは、どのような位置関係にあるのか。 ③対数関数のグラフにはどんな特徴があるのか。 ④対数計算の習熟。 | 一斉 | ・本時の学習課題を的確に把握させる。 ・指数関数の定義とグラフを引き合いに出しながら、本時の課題について説明する。 | 指数関数・対数関数のグラフと関連させて授業を進めるので、忘れているようなら復習する。 | 本時の目標を定めやる気を起こさせる。 コンピュータが出題する対数計算の問題を競争して解くことを告げ積極的な参加を促す。 | |
| 展開 42分 | 課題解決の取り組み | 対数関数の定義 | 一斉 | ・コンピュータのスイッチを入れさせる。 ・一斉送信により ムービル:24-LOG箱の対応の様子を見せる。 ・xにを対応させる関数として、対数関数を定義する。 | 底a,真数x(独立変数)について確認する。 | 生徒がモニターに集中するよう関心を高める。 |
| 対数関数のグラフ 対数関数のグラフと指数関数のグラフは直線y=xに関して対称である。 | 一斉 | ・プリントによりy=2xのグラフ上の任意の点P(a,b)をとる。このとき、対数の定義よりQ(b,a)はy=logaxのグラフ上の点であることを説明する。 点P(a,b)とQ(a,b)は直線y=xに関して対称であることを説明する。 y=2xのグラフとy=logaxのグラフは直線y=xに関して対称である。 | “任意”の意味をしっかり説明する。 直線PQとy=xは直行すること、直角三角形の合同を使い、わかりやすく説明する。 まず、y=2xとy=xを示し、対称に移動したらどうなるか予想させる。 | 黒板に図を書き、しっかりイメージが持てるよう配慮する。 生徒がモニターに集中するよう関心を高める。 | ||
| 対数関数のグラフの特徴 | ・底の値を変化させ、底の値とグラフの形の関係を説明し、グラフが必ず通る点、漸近線について確認する。 | 1(底の値)を境にグラフの形が大きく変わることを認識させる。 | ||||
| 演習:次のグラフを書け。 (1)y=log2x (2)y=log3x (3)y=log1/2x (4)y=log1/3x | 個別 | ・点(1,0)ともう1点の座標を取りグラフの概形をプリントに書かせる。 ・黒板にグラフを書き、確認させる。 | なめらかに漸近線に近づくように書かせる。 | 点をたくさん取って書くわけではないので、(1)から(4)のグラフをモニターに出し、書きやすくする。 | ||
| 対数関数の性質のまとめ | ・プリントと教科書97ページを参照しながらプリントに対数関数の性質をまとめる。 | |||||
| 演習 | 演習:次の対数関数の値を求めよ。 問題はコンピュータがランダムに出題する。 | 一斉 個別 | ・「数学教室-指数・対数関数」の起動手順、操作方法を説明する。 ・フロッピィを上のドライブに挿入しリセットさせる。 ・一斉にスタートさせ、対数の値を競争して求めさせる。 | 操作を一つ一つ確認できるよう手際よく説明する。 生徒の状況を見て個別に援助する。 | 評価には関係ないことを告げ、楽しい雰囲気で行えるよう配慮する。 | |
| 整理 3分 | まとめ | 本時の学習内容を再確認する。 | 一斉 | ・定義域・値域、底>1、0<底<1それぞれのグラフの概形とxが増加したときのyの増加・減少、必ず通る点、漸近線について発問する。 | 発問に答え、本時の学習内容を確認する。 | 内容を整理して定着をはかる。 | 次時の予告 | 教科書P98例11、例12 P99問9、練習17 | 一斉 | ・対数関数のグラフの平行移動、対数方程式・不等式を学習することを予告する。 | 復習事項、学習課題、欠時の学習内容を正確に把握させる。 | 次時の学習の準備をさせ、学習への動機付けをする。 |
3.使用したプリント
対数関数とそのグラフ
 a>0,a≠1のとき、正の数xに
a>0,a≠1のとき、正の数xに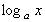 を対応させる関数
を対応させる関数
を、aを底とする対数関数という。
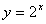
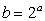

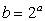
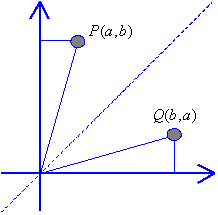
点Q(b,a)は 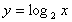

点P(a,b)と点Q(b,a)は直線 y=x に関して対称である。

点Pは指数関数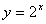
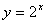
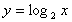
指数関数のグラフを y=x に関して対称に移動することにより、対数関数の グラフがどのような形になるのか、コンピューターで確かめてみよう。
◎対数関数のグラフ
次の対数関数のグラフを書きなさい。
(1)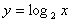 x=1のとき y= x=4のとき y= | (2)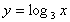 x=1のとき y= x=3のとき y= |
(3) x= のとき y= x= のとき y= | (4)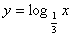 x= のとき y= x= のとき y= |
◎対数関数の性質
|
![]() 授業 実 施 後 の 感 想
授業 実 施 後 の 感 想
![]()
指数関数のグラフは、4日前の木曜日に、プリントを用意して一つ一つ点を取らせて書かせたのだが、あまり定着していなかった。
・値域 ・底とグラフの概形の関係
・漸近線 ・グラフが必ず通る点
といったことを忘れている者が多く、そのため、指数関数の復習を強く意識しながら授業を進めた。
コンピューターを利用することにより、
①対数関数のグラフは指数関数のグラフを直線y=xに関して対称に移動した物で あること。
②底が変化すると、それにつれて、グラフが変化する様子。
③グラフは、指数関数なら(0,1),対数関数なら(1,0)を必ず通ること。
については、画面を見て理屈抜きで視覚的にイメージを持つことができたようである。特に③は「なるほど」といった感じであった。
対数の値を求める競争の方は、最後の13分くらいの時間で行った。待ちきれなくて先にやろうとする者も出たが、リセットをかけ最初に戻させた。10問正解した者が優勝ということで、一斉にスタート。答えがあっていると歓声を上げる者や、難しい問題に悪戦苦闘して助けを求めてくる者など、大いに盛り上がった。
本間比呂志先生(夕張緑ケ丘実業高校)作成のソフトは、対数計算の問題はQ1からQ5に分類されている。なかなかおもしろくできていると思う。
・問題がランダムに作られるため、隣のパソコンと同じ問題にならない。
・見ただけですぐ答えられるような問題から落ち着いて計算しないとできない問題まで、順不同で出てくる。
(対数計算が苦手の者でも優勝するチャンスあり。)
・同じ問題を何回も間違うと、10問終わっても最初に戻ってしまう。
(当てずっぽうで答えられない。)
・学習の記録が残る。
といった点が特徴である。もしかしたら、問題を板書して演習させる方がじっくり取り組ませることができるのかもしれない。しかし、感情をあらわにしてはしゃいで取り組んでいる生徒の姿は、とても印象的であった。
このソフトを使うときには、Aドライブから起動しないと答えを入力する場所を示す ? が表示されないので、注意していただきたい。
全般的に、ちょっと時間が足りなかったが、生徒は一生懸命取り組んでいた。