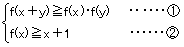| (1) | 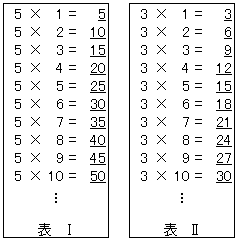 �@5�̔{���̉��ꌅ�i��̈ʁj�ׂ�ƁC�\�T�̂悤�ɁC0��5��������Ȃ��B����C3�̔{���̉��ꌅ�ׂ�ƁC�\�U�̂悤�ɁC�ꌅ�̐����i0�C1�C2�C����C9�j�����ׂĕ\���B���̕\�U�̗�̂悤�ɁC�ꌅ�̐����ł��̔{���̉��ꌅ��0�C1�C2�C�c�C9�̂��ׂĂ��������̂�S��������B �@5�̔{���̉��ꌅ�i��̈ʁj�ׂ�ƁC�\�T�̂悤�ɁC0��5��������Ȃ��B����C3�̔{���̉��ꌅ�ׂ�ƁC�\�U�̂悤�ɁC�ꌅ�̐����i0�C1�C2�C����C9�j�����ׂĕ\���B���̕\�U�̗�̂悤�ɁC�ꌅ�̐����ł��̔{���̉��ꌅ��0�C1�C2�C�c�C9�̂��ׂĂ��������̂�S��������B�@�k�����̐ݖ�(1)�̂݁C�v�Z��������������Ȃ��Ă��悢�B�l �@���ɐ��̐������̔{���̉��ɁC00�C01�C02�C�c�C99�̂��ׂĂ�����邩�ǂ����ׂ悤�B�i�������C00��0�C01��1�Ȃǂꎋ����B�j���̂��߂ɁC |
| (2) | �@���� �܂��� �܂��� �̔{���̂Ƃ��C�����̉��ɂ́C00�C01�C02�C�E�E�E�C99�̂��ׂĂ͌���Ȃ��B�ɓ��Ă͂܂�2���Ƃ��̗��R���q�ׂ�B�i�������C�ɓ��Ă͂܂鐔��100,200�Ȃǖ����ɂ���̂ŁC�ł��{���I�Ǝv����2���邱�ƁB�܂��C���R�͌����ȏؖ��łȂ��Ă��悢�B�j �̔{���̂Ƃ��C�����̉��ɂ́C00�C01�C02�C�E�E�E�C99�̂��ׂĂ͌���Ȃ��B�ɓ��Ă͂܂�2���Ƃ��̗��R���q�ׂ�B�i�������C�ɓ��Ă͂܂鐔��100,200�Ȃǖ����ɂ���̂ŁC�ł��{���I�Ǝv����2���邱�ƁB�܂��C���R�͌����ȏؖ��łȂ��Ă��悢�B�j |
| (3) | �@����(2)��2�� �C �C �̂�����̔{���ł��Ȃ��Ƃ��́C�����̉���00�C01�C02�C�E�E�E�C99�̂��ׂĂ������̂ł͂Ȃ����Ɗ��҂ł���B�������������̐������C���ɂ��Ă����Ƃ����̉����������Ƃ��C �̂�����̔{���ł��Ȃ��Ƃ��́C�����̉���00�C01�C02�C�E�E�E�C99�̂��ׂĂ������̂ł͂Ȃ����Ɗ��҂ł���B�������������̐������C���ɂ��Ă����Ƃ����̉����������Ƃ��C�@�@�@����-����=100���@�@�i���͐��̐����j �ƕ\�킹�邱�Ƃ�p���C��1�C��2�C��3�C�c�C��100�̒��ɉ������������̂�����Ɖ��肷��Ɩ����������邱�Ƃ��������Ƃɂ��C���̊��҂����������Ƃ��ؖ�����B |
| (4) | �@99�ȉ��̐��̐����ŁC���̔{���̉���00�C01�C02�C�c�C99�̂��ׂĂ��������̂͂������邩�B �@�k�����������łȂ��C�ȒP�ł悢����v�Z���������ƁB�l |
 ��1�i�K
��1�i�K ��2�i�K
��2�i�K ��3�i�K
��3�i�K
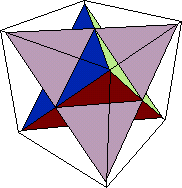 �@�@��2�i�K
�@�@��2�i�K
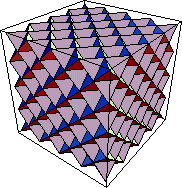 �@�@��4�i�K
�@�@��4�i�K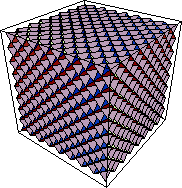
 �ɑ��āC�m(��)��
�ɑ��āC�m(��)��