（２）ＢＩ＝ＣＤで、ＢＩ⊥ＣＤであることを証明せよ。
この3つの正方形の中心を順に、Ｏ1，Ｏ2，Ｏ3とおく。
（３）辺ＢＣの中点Ｍを利用して、Ｏ1Ｏ2＝CＯ3で、Ｏ1Ｏ2⊥CＯ3であることを証明せよ。
線分ＦＩの中点をＮとする。
（４）ＡＯ3＝ＡＮ，ＡＯ3⊥ＡＮであることを証明せよ。
 |  |
 |  |
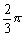
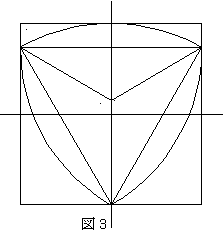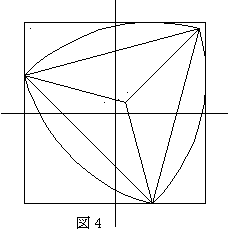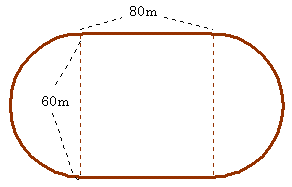
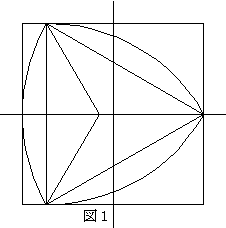
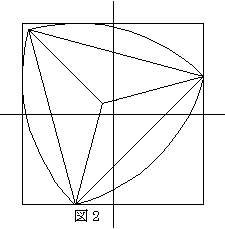
今、図１、図２、図３、図４の様に１辺の長さが２の正方形の内部を、ル−ロ−の三角形が反時計方向に回転するものとする。
問１
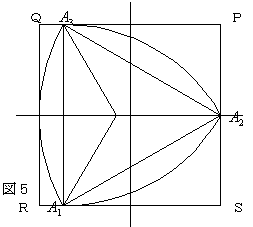
右図５の様にP（１，１），Ｑ（−１，１），Ｒ(−１，−１)，Ｓ（１，−１）なる正方形ＰＱＲＳの内部に、ル−ロ―三角形 Ａ1Ａ2Ａ3が存在する時、点Ａ1，Ａ2，Ａ3の重心Ｇの座標を求めよ。
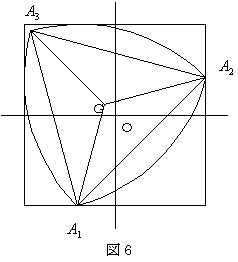右図６の様に、ル−ロ−の三角形が、正方形ＰＱＲＳの内部を、反時計に回転する時
問２
３０度回転した時の点Ａ1，Ａ2，Ａ3，重心Ｇの座標を求めよ。
問３
更に、３０度回転した時の点Ａ1，Ａ2，Ａ3，重心Ｇの座標を求めよ。
問４
ル−ロ−の三角形が、正方形の中で完全に1回転した時、重心Ｇが原点Ｏを中心に、円周のような道のまわりを何回、回転するか。
問５
以下同様に、正方形の内部を反時計まわりに回転する時、ｔ°(0≦ｔ≦30°)回転した時の重心Ｇのｘ座標、ｙ座標をｔを使って表せ。ただし、点Ｖ（ｘ，ｙ）を原点Ｏを中心にθ度回転した点をＷ（Ｘ，Ｙ）とすると、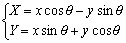
となる。
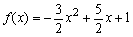は、ｆ(ａ)＝ｂ，ｆ(ｂ)＝ｃ，ｆ(ｃ)＝ａ（ａ，ｂ，ｃは整数）を満たしている、次の各問いに答えよ。（１）ａ≠ｂ，ｂ≠ｃ，ｃ≠ａを示せ。
（２）{ｘ｜ｆ(ｘ)＞ｘ}∩｛ａ，ｂ，ｃ｝≠φを示せ。
（３）ａ，ｂ，ｃを求めよ。
（１）Ｏから辺ＡＢに達し、さらに辺ＢＣで反射し、３回目でＯに戻るとき、角θを求めよ。
（２）辺ＡＢで反射し、１回目で頂点Ｃで止まるとき、tanθの値を求めよ。
（３）Ｏから各辺で２回反射し、ある頂点で止まるとき、tanθの値を求めよ。
（４）Ｏから各辺で５回反射し、ある頂点で止まるとき、経路が最も長くなる場合は、どの頂点に達するときで、その経路の長さはいくらか。
（５）Ｏから各辺で偶数回反射し、ある頂点に達する経路は、ただ1つであることを説明せよ。
