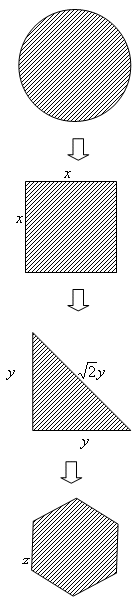
 乮侾乯偳傫側曄宍傪幚巤偟偰傕柺愊堦掕偱偁傞偺偱丄弶婜偺墌傪敿宎侾偺墌偲偟偰峫偊傞偲墌偺柺愊俽亖兾丆墌偺廃埻俴亖俀兾
乮侾乯偳傫側曄宍傪幚巤偟偰傕柺愊堦掕偱偁傞偺偱丄弶婜偺墌傪敿宎侾偺墌偲偟偰峫偊傞偲墌偺柺愊俽亖兾丆墌偺廃埻俴亖俀兾乮鶣乯偙偺墌偑惓曽宍偵曄宍偡傞偲偒
丂塃恾偺傛偆偵丄惓曽宍偺侾曈偺挿偝傪倶偲偡傞偲惓曽宍偺柺愊亖墌偺柺愊傛傝
丂丂丂倶2亖兾丂丂
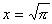
丂惓曽宍偺廃埻傪俙偲偡傞偲
丂丂丂
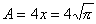
丂丂丂A2亖侾俇兾丂乧嘆
乮鶤乯偙偺墌偑捈妏擇摍曈嶰妏宍偵曄宍偡傞偲偒塃恾偺傛偆偵丄奺曈傪
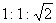 偺斾偵廬偭偰丄
偺斾偵廬偭偰丄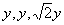 偲偡傞偲丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
偲偡傞偲丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂捈妏擇摍曈嶰妏宍偺柺愊亖倷2/俀亖兾丂丂
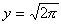
捈妏擇摍曈嶰妏宍偺廃埻傪俛偲偡傞偲
丂丂丂
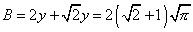
丂丂丂
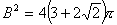 丂乧嘇
丂乧嘇乮鶥乯偙偺墌偑惓榋妏宍偵曄宍偡傞偲偒塃恾偺傛偆偵丄惓榋妏宍偺1曈偺挿偝傪倸偲偡傞偲
丂丂丂惓榋妏宍偺柺愊亖
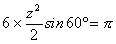 丂丂
丂丂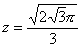
丂惓榋妏宍偺廃埻傪俠偲偡傞偲
丂丂丂
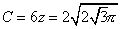
丂丂丂
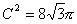 丂乧嘊
丂乧嘊嘆嘇嘊傛傝丄兾亖俁丆
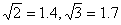 偲偟偰丄偍偍傛偦偺抣傪媮傔傞偲
偲偟偰丄偍偍傛偦偺抣傪媮傔傞偲丂丂丂俴2亖36丆俙2亖48丆俛2亖69.9丆俠2亖41.6
廬偭偰俴亙C亙俙亙俛偺戝彫偺弴斣偲側傝
丂丂丂墌偺廃埻亙惓榋妏宍亙惓曽宍亙捈妏擇摍曈嶰妏宍
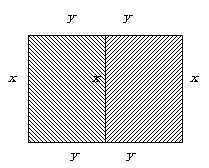
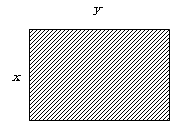 乮俀乯塃恾偺傛偆偵墶倷丆廲倶偺挿曽宍偵偮偄偰峫偊傞丅
乮俀乯塃恾偺傛偆偵墶倷丆廲倶偺挿曽宍偵偮偄偰峫偊傞丅丂丂丂挿曽宍偺柺愊亖倶亊倷亖倠乮掕悢乯
丂丂丂挿曽宍偺廃埻偺挿偝亖俀(倶亄倷)亖俀倶亄俀倷
俀倶亜侽丄俀倷亜侽傛傝丄亀憡壛暯嬒 憡忔暯嬒亁傛傝
丂丂丂
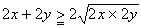
丂丂丂
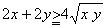
曄宍偵傛偭偰柺愊偼晄曄側偺偱丄倶亊倷亖倠傛傝丄
丂丂丂
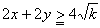
摍崋惉棫偼俀倶亖俀倷偺偲偒丄倶亖倷偺偲偒惓曽宍偺偲偒廃埻偺挿偝偼嵟彫偲側傞丅
丂丂丂廲丗墶亖侾丗侾
 乮俁乯塃恾偺條偵廲倶 丄墶倷偺俀偮偺椬愙偟偨挿曽宍偑偁傞丅偙偺椬愙偡傞俀屄偺挿曽宍偺廃埻偲嫬奅偺榓俴偲偡傞偲丄
乮俁乯塃恾偺條偵廲倶 丄墶倷偺俀偮偺椬愙偟偨挿曽宍偑偁傞丅偙偺椬愙偡傞俀屄偺挿曽宍偺廃埻偲嫬奅偺榓俴偲偡傞偲丄丂丂丂俴亖俁倶亄係倷
俁倶亜侽丄係倷亜侽傛傝亀憡壛暯嬒亞憡忔暯嬒亁偐傜
丂丂丂
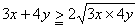
丂丂丂
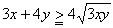
挿曽宍偺柺愊偼曄宍偵傛偭偰曄壔偟側偄偺偱丄倶倷亖倠乮掕悢乯
丂丂丂
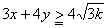
摍崋惉棫偼俁倶亖係倷偮傑傝丄倶丗倷亖係丗俁偺偲偒
椬愙偡傞俀屄偺挿曽宍偺廃埻偲嫬奅偺榓俴偼嵟彫偲側傝嵟彫抣偼
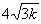
丂丂丂廲偲墶偺斾偼係丗俁
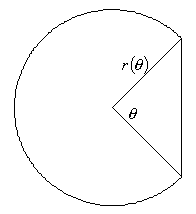 乮係乯曄宍慜偺偦傟偧傟偺墌偺敿宎傪侾偲偡傞丅塃恾偺傛偆偵丄侾偮偺媩宆恾宍偺敿宎傪倰(兤)偲偍偔
乮係乯曄宍慜偺偦傟偧傟偺墌偺敿宎傪侾偲偡傞丅塃恾偺傛偆偵丄侾偮偺媩宆恾宍偺敿宎傪倰(兤)偲偍偔丂丂丂侾偮偺媩宆偺柺愊亖
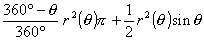 丂乧嘆
丂乧嘆偙偺侾偮偺媩宆恾宍偺柺愊偼曄宍偵傛偭偰曄壔偟側偄偺偱丄弶婜偺墌偺敿宎偼侾傛傝丄
丂丂丂柺愊偼兾乧嘇
嘆嘇傛傝
丂丂丂
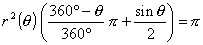
丂丂丂
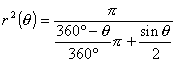 丂乧嘊
丂乧嘊嘊傊90亱丆120亱丆180亱傪戙擖偡傞偲
丂丂丂
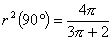 丂乧嘋
丂乧嘋丂丂丂
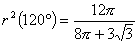 丂乧嘍
丂乧嘍丂丂丂
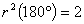 丂乧嘐
丂乧嘐壓恾偺傛偆偵椬愙偡傞俀偮偺媩宆偺恾宍偺嫬奅慄傪
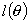 偲偡傞丅梋尫掕棟傛傝
偲偡傞丅梋尫掕棟傛傝丂丂丂
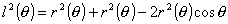
丂丂丂
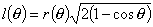 丂乧嘓
丂乧嘓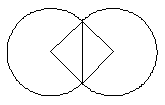 俀偮偺椬愙偡傞拞怱妏兤偺媩宆恾宍偺廃埻偲嫬奅慄偺榓傪俴(兤)偲偡傞偲
俀偮偺椬愙偡傞拞怱妏兤偺媩宆恾宍偺廃埻偲嫬奅慄偺榓傪俴(兤)偲偡傞偲丂丂丂
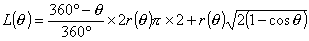 丂乧嘔
丂乧嘔嘔傊90亱丆120亱丆180亱傪戙擖偡傞偲
丂丂丂
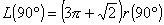
丂丂丂
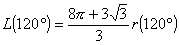
丂丂丂
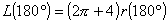
兾佮3偲偟偰椉曈傪俀忔偟偰戝彫傪斾妑偡傞偲
丂丂丂
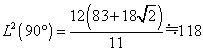
丂丂丂
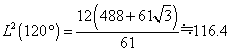
丂丂丂
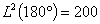
偲側傝兤亖120亱偺偲偒偑廃埻偲嫬奅慄偺榓偑嵟彫偲側傞丅