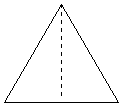
問題５ 【Fig-1】のような1辺の長さが４の正三角形ABCがある。
底辺BCの中点と点Ａを結ぶ線分で△ABCを切断し、【Fig-2】のような２つの合同な三角形△ABMと△DCEを作成する。
Ａ
Ａ Ｄ
Ｂ Ｃ Ｂ Ｍ Ｅ Ｃ
【Fig-1】 【Fig-2】
問1 △ABMと△DCEの底辺BMとECが一致するように重ねてできた【Fig-3】の多角形の面積を求めよ。
Ｄ Ａ
Ｂ(Ｅ) Ｍ(Ｃ)
【Fig-3】
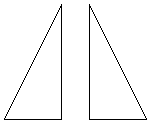
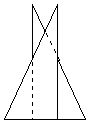
問2 △ABMと△DCEをBE＝α×BM（0＜α＜1）となるように底辺の一部が共有するように重ねてできた【Fig-4】の多角形の面積をＳ(α)とするとき、Ｓ(α)をαで表わせ。
Ａ Ｄ
Ｄ Ａ
Ｂ Ｍ Ｅ Ｃ B E M C
【Fig-4】
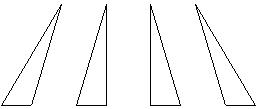
更に、この正三角形ABC【Fig-1】の底辺BCを4等分して、点Aと結ぶ線分で△ABCを切断し【Fig-5】のような４つの三角形△ABG,△DHI,△EJK,△FLCを作成する。
A A D E F
B C B G H I J K L C
【Fig-1】 【Fig-5】
問3 2つの三角形△ABGと△DHIについて、BH＝α×BG（0＜α＜1）となるよう底辺の一部が共有するように重ねてできた【Fig-6】の多角形の面積をT(α)とするとき、T(α)をαで表わせ。
D A
B H G I
【Fig-6】
問4 ４つの三角形４つの三角形△ABG,△DHI,△EJK,△FLCについて
BH＝α×BG,HJ＝α×HI,JL＝α×JK（0＜α＜1）となるよう底辺の一部が共有するように重ねてできた【Fig-7】の多角形の面積をU(α)とするとき、U(α)をαで表わせ。また、U(α)の最小値とそのときのαの値を求めよ。
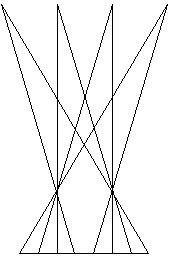F E D A
B H J
L G I K C
【Fig-7】
《注意》持参した、｢はさみ｣や｢のり｣等を利用して考えても良い。
また、答案用紙に切り取った図形等を貼り付けて解答しても良い。