| ■基本事項 |
| 学年／科目／単元 | １学年／数学Ⅰ／2次関数 |
| 学校名／作成者／作成年月日 | 札幌新川高校／早苗雅史／2004.3.21 |
| 実施形態／実施上の留意事項 | プレゼンテーション／特になし |
| GRPSバージョン／ファイルダウンロード | 6.32／bunri.gps(3KB) |
| ■題材の内容 |
| 方程式 x2-2mx+m+2=0 が1より大きな異なる2つの解を持つように，mの値の範囲を定めよ。 |
| ■題材のねらい |
| 判別式が正，軸が1より大，x=1のときの符号が正，という基本的な解法ではなく，固定された2次関数と1点を通る直線の交点を考えることでmの値の範囲を定める。 |
| ■学習の流れ |
| 【展開１】 | |
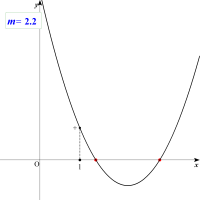
| この手の問題は普通は①判別式が正，②軸が1より大，③x=1のときの符号が正，という3つの条件を連立させて解くのが一般的ですが，これを別な角度から考えて見ましょう。 。 |  |
| 【展開２】 | |
|
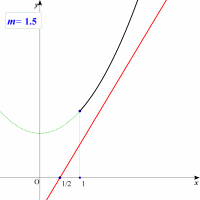
方程式を次のように変形します。 x2+2=m(2x-1) x>1 で2つの解を持つということは，2つのグラフ y=x2+2，y=m(2x-1) が，x>1 で2点で交わることと同値です。 |
 |
| 【展開３】 | |
|
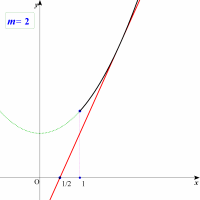
2つのグラフ y=x2+2，y=m(2x-1) のうち，y=x2+2 は固定されたグラフになります。y=m(2x-1) は定点 (1/2, 0) を通るグラフだということに注意してください。x>1 より y=x2+2 のx>1 の部分を考えます。 それではパラメータmを変化させ，2つのグラフが2点で交わる場合を考えます。mの値を大きくすると，あるところで1点で接します。このときのmの値は判別式が0になるときですから， D/4=m2-m-2=0 m>0より ∴m=2 |
|
| 【展開４】 | |
|
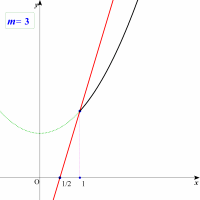
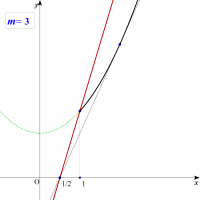
更にmの値を大きくすると，しばらくは2点で交わる状態が続きます。それでは次に共有点が1点しかない場合は，どんなときでしょう。 y=x2+2 上の点 (1, 3) を通るときですね。y=m(2x-1) が(1, 3)を通るときのmの値は 3=m(2-1) ∴m=3 |
 |
| 【展開５】 | |
|
つまり y=x2+2 (x>1)，y=m(2x-1) が2つの共有点を持つのは，2つの接する場合とy=m(2x-1) が(1, 3)を通るときを考えて 2 < m < 3 |
 |
| ■留意点・工夫点 |
|