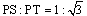f'(x)=3ax2+cより
f(x)が極値をもつ -3ac>0 ⇔ ac<0
3次関数f(x)=ax3+cx(ac<0)・・・①の基本性質
Ⅰ.f(x)は奇関数である。(y=f(x)のグラフは原点に関して対称)
Ⅱ.f(x)は極値をもつ。
f(x)=ax3+cx=x(ax2+c)=0より
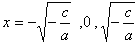 (点Aのx座標)
(点Aのx座標)f'(x)=3ax2+c=0より
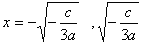 (点Cのx座標)
(点Cのx座標)よって
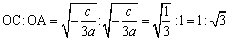
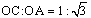 である。・・・・重要性質Ⅰ である。・・・・重要性質Ⅰ
|
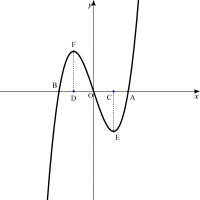
y=f'(t)(x-t)+f(t)
=(3at2+c)(x-t)+at3+ct
=(3at2+c)x-2at3・・・②
①、②の交点をHとするとき、y=ax3+cx,y=(3at2+c)x-2at3より
ax3+cx-(3at2x+cx-2at3)=0
a(x3-3t2x+2t3)=0
a(x-t)2(x+2t)=0
x=t,-2t(Hのx座標)
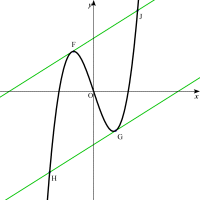
y=f'(-t)(x+t)+f(-t)
=(3at2+c)(x+t)-at3-ct
=(3at2+c)x+2at3・・・③(③と②は平行である。)
①、③の交点をJとするとき、
y=ax3+cx,y=(3at2+c)x+2at3より
ax3+cx-(3at2x+cx+2at3)=0
a(x3-3t2x-2t3)=0
a(x+t)2(x-2t)=0
x=-t,2t(Jのx座標)
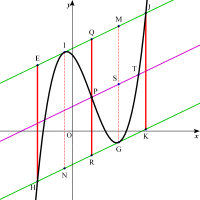
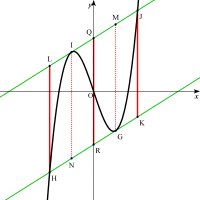
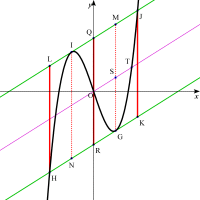
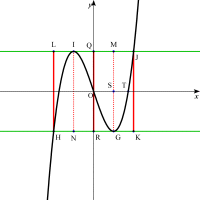
y軸に平行な線分JK,HL,GM,INとy軸上に線分QRをひくと
| 平行四辺形JKHLの中に4つの合同な平行四辺形JKGM、MGRQ、QRNI、INHLができる。・・・・重要性質Ⅱ |
なぜならば直線②と③は平行であり、点J,G,I,Hのx座標はそれぞれ2t,t,-t,-2tであるから。
y=(3at2+c)x・・・④
①、④の交点をTとするとき、y=ax3+cx,y=(3at2+c)xより
ax3+cx-(3at2x+cx)=0
a(x3-3t2x)=0
ax(x2-3t2)=0
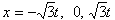 (Tのx座標)
(Tのx座標)また、④と線分GMの交点Sのx座標はtであるから
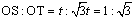 ・・・重要性質Ⅲ ・・・重要性質Ⅲ
|
以上より、
3次関数f(x)=ax3+cx(ac<0)・・・①と3直線②、③、④と5線分JK、GM、QR、IN、HLによって、8つの合同な平行四辺形ができる。また、④と線分GMの交点、④と①の交点をそれぞれS、Tとすると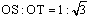 である。(重要性質のまとめ) である。(重要性質のまとめ)
|
f'(x)=3ax2+2bx+cよりb2-3ac>0のときf(x)は極値もつ。
3次関数f(x)=ax3+bx2+cx+d(b2-3ac>0)・・・⑤にたいして
f”(x)=6ax+2b=0よりx=-b/3a
y=f(x)の変曲点
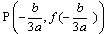 が原点にくるようにグラフを平行移動すると、
が原点にくるようにグラフを平行移動すると、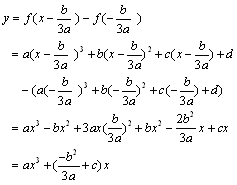
ここでb2-3ac>0であるから
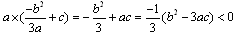 より
より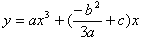 ・・・⑥はf(x)=ax3+cx(ac<0)・・・①型である。
・・・⑥はf(x)=ax3+cx(ac<0)・・・①型である。
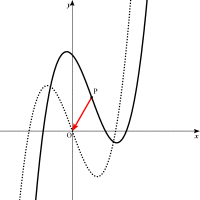
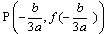 とすると
とすると
|
y=f(x)のグラフについて 基本性質 Ⅰ.y=f(x)のグラフはPに関して点対称である。 Ⅱ.f(x)は極値をもつ。
重要性質 |