| 【展開1】 |
|
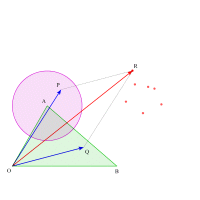
2つのベクトルが共に動くので,なかなかイメージしづらいところがありますね。いくつか端点を動かして自分なりにイメージしてみましょう。
|
 |
| 【展開2】 |
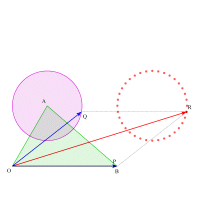
両方を闇雲に動かしてもなかなかわかりづらいので,一方を固定して,一方だけをを動かしてみましょう。点Pを頂点Bに固定し,更に点Qを円周上で動かしてみます。このときの終点はどんな軌跡を描くでしょうか。
アニメーションで見てみましょう。どうですか。円を描くのがわかりますね。そしてこの円はOBの長さの分だけ平行移動しているのです。
|
 |
| 【展開3】 |
|
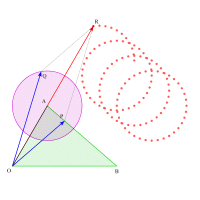
更に点Pも三角形の辺BA上にそって移動させてみましょう。先ほどの円がどんどん平行移動してのがわかります。
|
 |
| 【展開4】 |
|
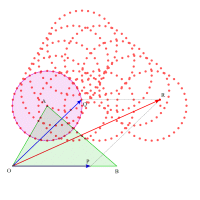
さらに三角形の辺を一周させると,求める領域が姿を現してきました。
|
 |
| 【展開5】 |
|
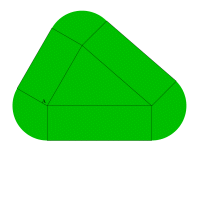
どうですか。△OABを平行移動し,3つの頂点を中心とした円を取り巻くように領域を描くのがわかります。
|
 |
| 【展開6】 |
|
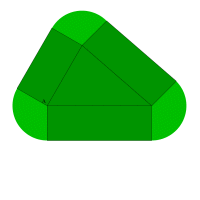
ではこの領域の面積はどのように求めたらよいでしょう。この領域は三角形が1つ,長方形が3つと扇形が3つで成り立っています。三角形の面積,長方形の面積は面積の公式や余弦定理を用いて出すことができます。扇形の面積はどうでしょう。右図の様に扇形以外の部分を取り除き,3つの扇形を合わせると1つの円になりますね。半径は1ですから面積は簡単に求めることができます。
|
 |
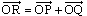 の終点Rが動く領域の面積を求めよ。
の終点Rが動く領域の面積を求めよ。
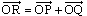 の終点Rが動く領域の面積を求めよ。
の終点Rが動く領域の面積を求めよ。





