y-t2=-1/2t・(x-t) ∴ y=-x/2t+t2+1/2
この法線が点(p, 3p+1/2)を通ることから,代入して
2t3-6pt2-p=0
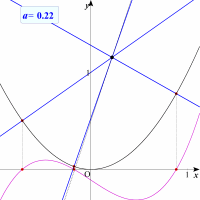
の方程式の解の個数と同じになります。実際に関数y=2t3-6pt2-pを同時に描画して,x軸との交点の様子を考察してみましょう。
| ■基本事項 |
| 学年/科目/単元 | 2学年/数学Ⅱ/微分 |
| 学校名/作成者/作成年月日 | 札幌新川高校/早苗雅史/2004.3.21 |
| 実施形態/実施上の留意事項 | プレゼンテーション/特になし |
| GRPSバージョン/ファイルダウンロード | 6.32/housen.gps(5KB) |
| ■題材の内容 |
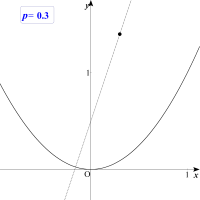
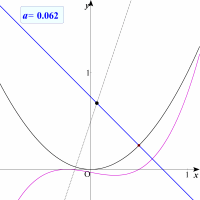
| 直線 y=3x+1/2 上の点 (p,q) から放物線 y=x2 の法線は何本引けるか調べよ。 |
| ■題材のねらい |
| 直線上の点から放物線への法線が何本引けるかをイメージ化させ,方程式との関連を考察させる。 |
| ■学習の流れ |
| 【展開1】 | |
| まずどんな法線が引けるかを考えて見ましょう。直線上のいろいろな点に対して,放物線へ何本引けるかイメージできますか。案外,難しいことが分かりますね。 |  |
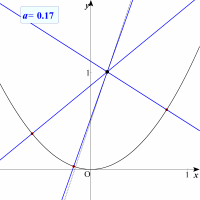
| 【展開2】 | |
| 最大3本引ける場合があります。しかし,直線上の点をどんどん下に下げていくと,2本しか引けない場合や1本しか引けない場合が存在します。 |  |
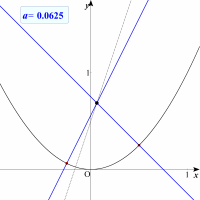
| 【展開3】 | |
| 直線上の点を自動で移動させ,その様子を見て見ましょう。3本から2本,そして1本へと法線が変化していく様子がよく分かります。 | 
|
| 【展開4】 | |
|
さてこの法線の本数をどのように場合わけすればよいでしょうか。点(p, 3p+1/2)から放物線 y=x2 に引いた接点を (t, t2)とすると,法線の方程式は y-t2=-1/2t・(x-t) ∴ y=-x/2t+t2+1/2 この法線が点(p, 3p+1/2)を通ることから,代入して 2t3-6pt2-p=0 の方程式の解の個数と同じになります。実際に関数y=2t3-6pt2-pを同時に描画して,x軸との交点の様子を考察してみましょう。 |
 |
| 【展開5】 | |
| 先ほどと同様に自動的に変数を変え,今度は3次関数とx軸との交点の様子を見てみます。どうですか,法線の引かされるx座標とと3次関数との交点のx座標が一致しているのが見て取れます。つまりこの問題は3次関数の解の個数を求める問題と同じであったことが分かります。 |  |
| ■留意点・工夫点 |
|