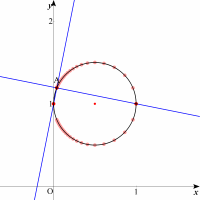
この円の方程式を求めるには直線g:y=ax+1と点(1, 1)を通り直線gと垂直な直線 y=-x/a+1/a+1(a≠0)の連立方程式を解き,パラメータaを消去する必要があります。しかし2点(0, 1),(1, 1)を直径とする円であることに気づけば,簡単に求めることができます。また,1点(0, 1)を除く事の意味も理解できるでしょう。
| ■基本事項 |
| 学年/科目/単元 | 2学年/数学Ⅱ/図形と方程式 |
| 学校名/作成者/作成年月日 | 札幌新川高校/早苗雅史/2004.3.19,2005.6.30 |
| 実施形態/実施上の留意事項 | プレゼンテーション/特になし |
| GRPSバージョン/ファイルダウンロード | 6.41/pt_kiseki.gps(3KB) |
| ■題材の内容 |
| 点 (1,1) を通る直線hと直線 g:y=ax+1 とが交点Aで垂直に交わるとする。aが実数全体を動くとき,交点Aの座標および軌跡を求めよ。 |
| ■学習の流れ |
| 【展開1】 | |
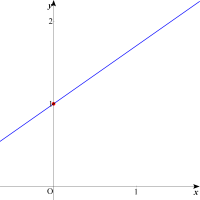
| まずパラメータaを変化させることで直線g:y=ax+1がどんな直線を描くのかを確認してみましょう。パラメータaが変化しても点(0, 1)を通ることが確認できます。式の上から,どうしたらその点が出てくるのか考えて見ましょう。 |  |
| 【展開2】 | |
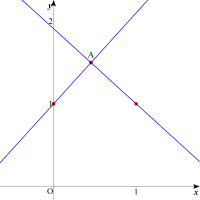
| 点(1, 1)を通り,直線gに垂直な直線をイメージしてみましょう。パラメータを変化させ,直線と交点の様子を観察します。 |  |
| 【展開3】 | |
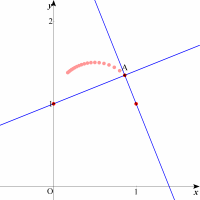
| 交点に残像をつけて,交点の描く軌跡を考察します。交点の軌跡は円になりそうなのがイメージできます。 |  |
| 【展開4】 | |
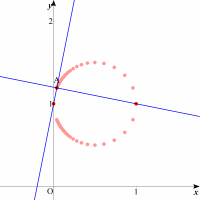
| それではパラメータを自動で変化させて見ましょう。ここで点の動く速度に注意して見てみてください。パラメータaがかなり大きくなると,少し遅くなりますね。またいくら大きくしても点(0, 1)に近づきそうで決して近づきません。それは直線の傾きがいくら小さくなっても,y軸にはならないからです。 |  |
| 【展開5】 | |
|
求める軌跡は円になりそうです。しかも1点(0, 1)を除いた円であることが予想されます。 この円の方程式を求めるには直線g:y=ax+1と点(1, 1)を通り直線gと垂直な直線 y=-x/a+1/a+1(a≠0)の連立方程式を解き,パラメータaを消去する必要があります。しかし2点(0, 1),(1, 1)を直径とする円であることに気づけば,簡単に求めることができます。また,1点(0, 1)を除く事の意味も理解できるでしょう。 |
 |
| ■留意点・工夫点 |
|