x+y=u,xy=vとおくと,x2+y2=1よりu2-2v=1
x+y=u,xy=vとおくと,x2+y2≦1よりu2-2v≦1・・・①
と一つの領域しか得られませんが,コンピュ-タの表す図形はもう一つあります。その実態は何でしょうか。問題に使われている式は円の方程式だけなのです。
x+y=u,xy=vとおくとx,yはt2-ut+v=0の解であるから
D=u2-4v≧0・・・②
先ほどの円を動かした領域①とこの点(x+y,xy)の表す領域②で求める解が得られるのです。
| ■基本事項 |
| 学年/科目/単元 | 2学年/数学Ⅱ/図形と方程式 |
| 学校名/作成者/作成年月日 | 札幌新川高校/早苗雅史/2003.11.3 |
| 実施形態/実施上の留意事項 | プレゼンテーション/特になし |
| GRPSバージョン/ファイルダウンロード | 6.22/ryouiki_f.gps(4KB) |
| ■題材の内容 |
| 点(x,y)が原点を中心とした半径1の円の周上及び内部を動くとき,点(x+y,xy)の動く領域を図示せよ。 |
| ■学習の流れ |
| 【展開1】 | |
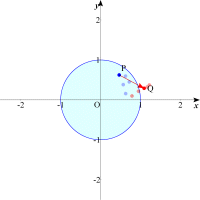
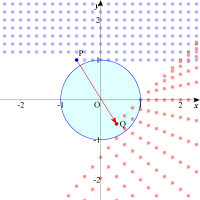
| まず題意を把握するために,具体的に円周上の点を動かしながら点(x+y,xy)をプロットしていくことでイメ-ジを膨らませてみましょう。円内の点P(x,y)に対して(x+y,xy)を対応させたのが,矢印の先の点Qです。いくつか試してみましょう。 |  |
| 【展開2】 | |
|
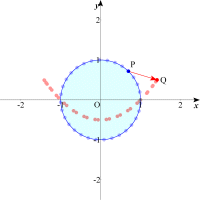
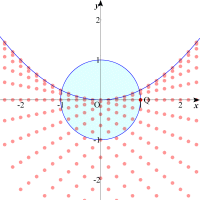
普通は図形の周上を動かすと答えが得られますね。では円周上の点を変換させてみましょう。すると一つの放物線らしきものが姿を現しました。この曲線の式は次の様にして求められます。 x+y=u,xy=vとおくと,x2+y2=1よりu2-2v=1 |
 |
| 【展開3】 | |
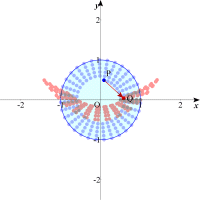
| 実は求める領域はこれだけではないのです。先ほどは円周上の点だけを変換しましたが,円の内部の点も変換してみましょう。どのようにしたら変換できるでしょう。円の半径をどんどん小さくして,先ほどと同様に円周上の点を変換させていけばよいのです。 |  |
| 【展開4】 | |
|
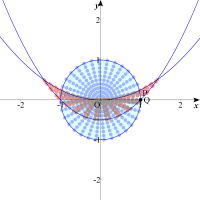
すると現れたのは二つの図形にはさまれた領域です。一つは先ほどの放物線です。領域でいうと x+y=u,xy=vとおくと,x2+y2≦1よりu2-2v≦1・・・① と一つの領域しか得られませんが,コンピュ-タの表す図形はもう一つあります。その実態は何でしょうか。問題に使われている式は円の方程式だけなのです。 |
 |
| 【展開5】 | |
| 実は点(x+y,xy)のとりうる領域は,「円の周上及び内部」という条件に関係なく,ある一定の図形を描くのです。実際に平面全体を一定の間隔で(x+y,xy)の点へ全て動かしてみよう。 |  |
| 【展開6】 | |
|
”実数x,y”という条件だけで,既に点(x+y,xy)はある領域を表していたのです。この“実数”という条件は式の上では, x+y=u,xy=vとおくとx,yはt2-ut+v=0の解であるから D=u2-4v≧0・・・② 先ほどの円を動かした領域①とこの点(x+y,xy)の表す領域②で求める解が得られるのです。 |
 |
| ■留意点・工夫点 |
|
| ■参考ページ |