定点を通る曲線

円 x2＋y2−2ax−4ay＋10a−10＝0が，定数aの値に関わらず通る2定点を求めよ。またこれらの円のうち，半径が最小となる時のaの値を求めよ。

■学習の流れ

【展開１】
まずこの問題の意味を把握しましょう。そのために，aに簡単な値（例えばa=‐1，0，1あたりから）を代入してグラフがどうなるかを調べてみましょう。
【展開２】
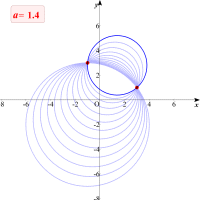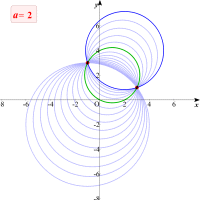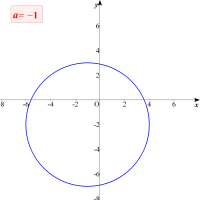
次にパラメータaを変化させながら，軌跡を取ることでグラフの変化する様子を調べてみましょう。この様子から確かに２定点を通るのがわかりますね。 さてこの２定点はどのように求めればよいでしょう。交点を求めるためには２つの円があれば十分です。計算が簡単なa=0，1のときの方程式 　x2＋y2−10＝0，x2＋y2−2x−4y＋10＝0 を連立させれば出すことができます。 またこの問題は任意のaについて成り立つわけですから，aの恒等式と見て 　(x2＋y2−10)＋(−2x−4y＋10)a＝0 として 　x2＋y2−10＝0，−2x−4y＋10＝0 を解いても求めることができます。先ほどの2つのaの値から求める方法は恒等式の解法の「数値代入法」，後者の方法は「係数比較法」にあたります。
【展開３】
またこの2点がわかれば，最小となる円がその2点を直径とする円であることがわかりますね。このことから，半径が最小の時のaの値を求めることができます。

■留意点・工夫点

【展開１】でスクリプトを用いて軌跡の様子を提示する。

■参考ページ

気軽にもっとGRAPES（早苗雅史）