| 亂揥奐侾亃 |
|
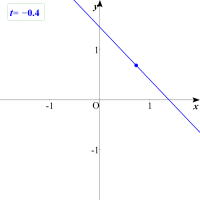
傑偢栤戣偺堄枴傪攃埇偡傞偨傔偵丆嬶懱揑偵t偵悢抣傪擖傟偰捈慄偑偳偆側傞偐妋偐傔偰傒傑偟傚偆丅
|
 |
| 亂揥奐俀亃 |
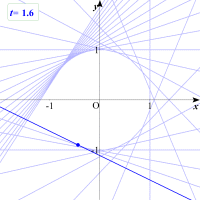
峏偵婳愓傪巆偡偙偲偱丆偙偺捈慄偑偳偆偄偭偨嬋慄偵愙偡傞偺偐偑傢偐傝傑偡丅弌偰偒偨恾宍偑墌偱偁傞偙偲偑傢偐傝傑偡偹丅
偙偺墌偺曽掱幃偼偳偺傛偆偵媮傔傞偙偲偑偱偒傞偱偟傚偆丅曽掱幃傪師偺條偵曄宍偟傑偡丅
丂丂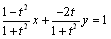
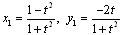 偲偍偔偲 偲偍偔偲
丂丂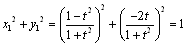
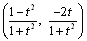 偵偍偄偰丆墌x2+y2=1偵愙偡傞偙偲偑傢偐傝傑偡丅 偵偍偄偰丆墌x2+y2=1偵愙偡傞偙偲偑傢偐傝傑偡丅
|
 |
| 亂揥奐俁亃 |
師偵t偑t亞1偺斖埻傪摦偔偲偒偺捈慄偺捠夁偡傞斖埻傪媮傔偰傒傑偟傚偆丅愙揰偺x嵗昗傪師偺傛偆偵曄宍偟傑偡丅
丂丂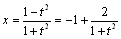
t亞1傛傝-1亙x亝0偑摫偐傟傑偡丅偙偙偱偄偔傜t傪戝偒偔偟偰傕-1偵偼側傜側偄偙偲偵拲堄偟傑偟傚偆丅摨條偵愙揰偺y嵗昗傕師偺條偵曄宍偟傑偡丅
丂丂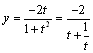
偙偙偱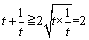 偵拲堄偡傟偽-1亝y亙0偑摫偐傟傑偡丅 偵拲堄偡傟偽-1亝y亙0偑摫偐傟傑偡丅
偮傑傝墌偺戞3徾尷偺晹暘偵愙偡傞捈慄偑捠夁偡傞椞堟傪峫偊傟偽椙偄偙偲偵側傝傑偡丅
|
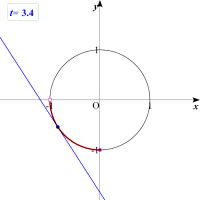 |
| 亂揥奐係亃 |
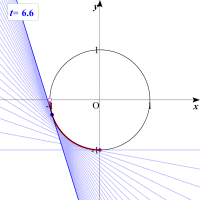
墌偺戞3徾尷偺晹暘偵愙偡傞捈慄偑捠夁偡傞椞堟偼偳偆側傞偱偟傚偆丅傕偆堦搙婳愓傪庢傞偙偲偱妋擣偟偰傒傑偟傚偆丅
僷儔儊乕僞t傪偳傫偳傫戝偒偔偟偰偄偒傑偡丅t傪戝偒偔偡傞偲捈慄偺乬摦偒乭偑抶偔側偭偰偒傑偟偨丅捈慄偺枾搙傕崅偔側偭偰偒傑偟偨偹丅
|
 |
| 亂揥奐俆亃 |
|
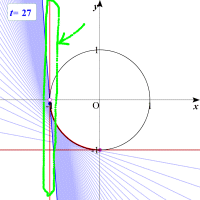
媮傔傞椞堟偼塃恾偺傛偆偵側傞偺偱偡偑丆偙偙偱t傪偄偔傜戝偒偔偟偰傕捈慄x=-1偵偼側傜側偄偺偵拲堄偟偰偔偩偝偄丅愭傎偳愙揰偺x嵗昗偑-1亙x亝0偱偁傞偙偲傪媮傔傑偟偨偑丆x=-1偑擖傜側偄偺偑僌儔僼偺曄壔偐傜傕僀儊乕僕偡傞偙偲偑偱偒傑偡偹丅
|
 |

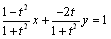
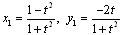 偲偍偔偲
偲偍偔偲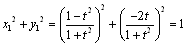
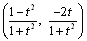 偵偍偄偰丆墌x2+y2=1偵愙偡傞偙偲偑傢偐傝傑偡丅
偵偍偄偰丆墌x2+y2=1偵愙偡傞偙偲偑傢偐傝傑偡丅
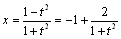
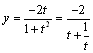
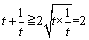 偵拲堄偡傟偽-1亝y亙0偑摫偐傟傑偡丅
偵拲堄偡傟偽-1亝y亙0偑摫偐傟傑偡丅

