方程式の解とグラフ

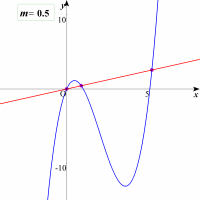
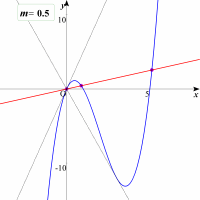
曲線y＝x3−6x2＋5x と直線 y＝mx とが相異なる3点で交わるためのmの条件を求めよ。

■題材のねらい

３次曲線と直線の交点が３個あるための条件を求める問題であるが，一組の答えはすぐにイメージできる。しかしもう一組の答えはイメージしずらい。ズーム機能を用いることでイメージ化させる。

■学習の流れ

【展開１】
パラメータmを変化させて交点が３個できる場合をイメージして見ましょう。そんなに難しくはありませんね。しかし３個持つパターンが２パターンあるのがイメージできますか？
【展開２】
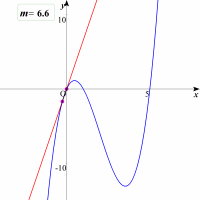
実はかなり局所的に観察しないといけないんです。パラメータmの値をどんどん大きくしてみましょう。すると少し分かりづらいのですが，交点を３個持つ場合がわかるでしょうか。
【展開３】
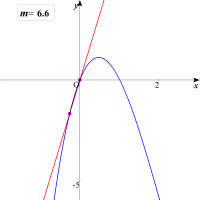
少し分かりづらいので，その部分を拡大してみましょう。
【展開４】
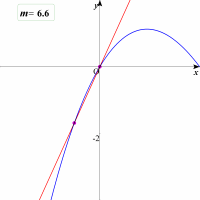
更に拡大して見ましょう。どうです確かに交点が３個あるのが分かりますね。
【展開５】
曲線y＝x3−6x2＋5x と直線 y＝mxを連立させると，まず交点の一つ原点が出てきます。残る2つは判別式を取ることで求めることができますが，mの範囲が2個出てくる理由がイメージできます。

■留意点・工夫点

この問題の答えは −4＜m＜5，5＜m と2つに分かれます。一見するとどうして2つに分かれるのかイメージしづらいところがあります。原点からの接線1本と原点における接線の2本を補助線としてパラメータを変化させ，m＝5 近辺の様子をZOOMさせてみましょう。確かに交点が3つあるのが見て取れます。 Grapeseファイルを作成するときに展開ごとにスクリプトを組むことで，ZOOMさせる展開が非常にスムーズに進みます。