では、このソフトの数学への応用について考えてみよう。もちろん、デカルト座標上の陰関数、陽関数、極座標上のサイクロイド、レムニスケートといった曲線は簡単に描画できるが、「絵定義」の機能を最大限活かそうと考えるならば、本ソフトは、複素数による図形変換を視覚的に提示するのに最適である。
現教育課程になって、複素数平面の指導は、高校時代授業で習ったことのない世代が教師として教えることも多く、少なからずその指導法に関しては現場で混乱をきたしている。複素数の指導には３つのアプローチがあるかと思うが、メディア世代の生徒にとっては、その中で、複素数をオペレータと捉えた図形変換としてのアプローチが一番理解しやすいであろう。ただ、それを視覚化しようとするとやはりそれ相応の苦労はついてまわるのであるが、このBASICはその苦労を解消してくれるのである。
例えば、ω＝ａ＋ｂｉなる複素数をｚに乗じてみよう。ωを極座標に変換してみると、
と表わされる。ｚも同様に変換すると、ｚはωにより複素数平面上で、原点に対して、ｒ倍の拡大、θの回転をすることが分かる。この拡大や回転を十進BASICで考えると、図形としてのｚにzukeiのような名前をつけて「絵定義」し、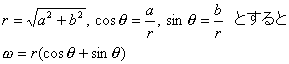
これを利用して、例えば、 をグラフィックスとして描画してみると下図のような綺麗な模様が浮かびあがってくる。
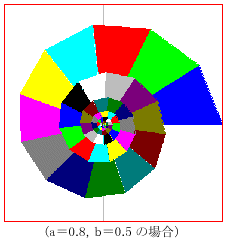
ａ，ｂの値をいろいろ変えて描画すると、万華鏡を覗いているような、極彩色の世界が繰り広げられる。
(この話題は、前回の数実研での石狩南高校の清水先生の授業実践によるアイデアをプログラム化したものである。)
さて、いくつかの例を示そう。
右図は、絵定義によって描いた「家」を複素数変換したものである。
回転、拡大の順で処理している。本BASICには、点を結んで描かれた図形の内部を塗りつぶす機能がある。これを利用して、部品として、煙突、窓、玄関、屋根を作り、角度θの大きさまで連続して変化させ描画するとアニメ的に表示される。同様のことを拡大率ｒまで変化させてやればよい。ただ、この場合、変化の過程の残像が残ってしまい、見にくい印象を与えるかもしれない。
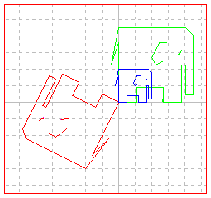右図は、象(象の像というつまらない洒落であるが)を絵定義し、複素数変換したものであるが、家の図形の変換とは若干異なる。変換の過程が、拡大、回転であることと、もう一つは残像を残していない。
実は十進BASICには、旧BASICにあったSCREEN文による画面の切替えがない。通常、残像を消去するには、SCREEN文によって、画像を交互に描き、一方が表示されているときに他方を消してしまえばよい。そうすると視覚的には図は動いているように変化するのである。
このソフトにはＣＬＥＡＲ文というグラフィックス画面全体を消去する命令はあるのだが、いちいちクリアするとどうしても画面はちらついてしまう。そこで、別の方法である工夫をしてこのプログラムは像を描いている。どうするのかというと、残像を消すと考えずに、残像を改めて描いてやると考えればよい。お分かりだろうか？。