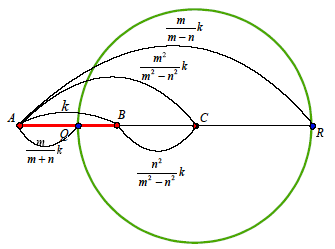
アポロニウスの円の中心と半径
札幌旭丘高校 中村文則
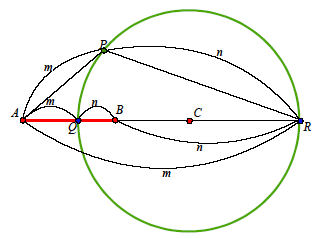 2点A,Bからの距離の比がm:n(m≠n)である点の軌跡は,ABをm2:n2に外分する点Cを中心とし,半径
2点A,Bからの距離の比がm:n(m≠n)である点の軌跡は,ABをm2:n2に外分する点Cを中心とし,半径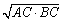 である円である. である円である.
|
Proof)
複素数平面上で軌跡を考える.
A(α),B(β)とし,動点をP(z)とする.
AP:BP=m:nより,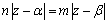 である.
である.
両辺を平方して,式変形する.
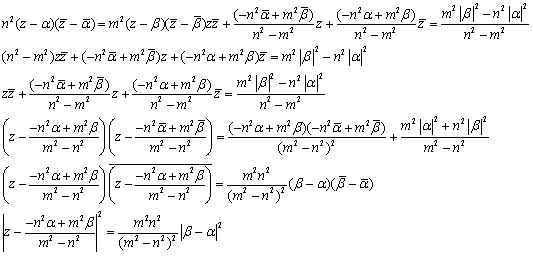
 これより,P(z)は,中心
これより,P(z)は,中心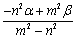 ,半径
,半径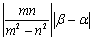 である円を表す.
である円を表す.
よって,求める軌跡は円であり,その中心は線分ABをm2:n2の比に外分する点である.
次に,AB=k,m>nとすると,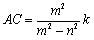 であるから,
であるから,
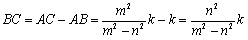
円の半径をrとすると,
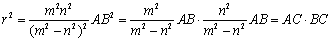
のときも同様であるから,ゆえに,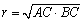 である. Q.E.D
である. Q.E.D
|
ex)A(2,1),B(-4,-2)に対して,AP:PB=1:2を満たす点Pの軌跡を求めよ. (センター試験追試)
|
解) 中心(x,y)はABを1:4の比に外分する点より,
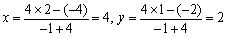
∴ C(4,2)
また,中心rは,
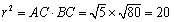 より,
より,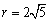
以上より,求める軌跡は,中心(4,2)で半径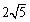 の円である.
の円である.
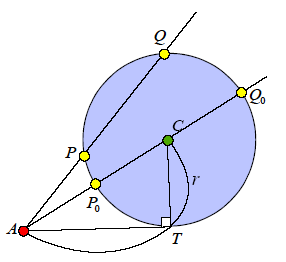 なお,点 からアポロニュースの円に引いた直線と円との交点をP,Qとすると,方べきの定理より,
なお,点 からアポロニュースの円に引いた直線と円との交点をP,Qとすると,方べきの定理より,
AP・AQ=(一定)
である.その値は,点Aから円に引いた接線の接点をTとするとき,AT2に等しい.よって,
AP・AQ=AT2=AC2-r2
ここで,アポロニウスの円の性質より,r2=AC・BC であるから,
AP・AQ=AC2-AC・BC=AC(AC-BC)=AC・AB
これは,円と円外の点が与えられたとき,その円をアポロニウスの円として生成する元の線分ABが求められることを意味する.また,その比の値は,直線ACが円と交わる2点をP0,Q0とするとき,
AQ0+AP0:AQ0-AP0
で与えられる.
ひと言
アポロニウスの円に関する本文の性質は2年ほど前に見つけたものである.当時,けっこう美しくまとまったことで,悦に入り,少し発展させようと試みて,参考文献をインターネットで検索したら,
アポロニウスの円~定義を少し広げる試み~ 愛知県立高浜高等学校 山崎博司
にヒットした.
なんとその内容は,本文の円の中心の求め方が,既に「数研通信」(№33)に掲載されていることを延べていた.さらに,山崎氏は別角度から,2つの円までの接線の長さの比が一定である点の軌跡を利用し,点を点円と捉えて鮮やかな解法を導き出していた.そして,何よりも驚いたのは,そのレポートの掲載元は「数学のいずみ」であった.
山崎先生は,数実研に出席したことはない.したがって氏のレポートはインターネットで数学のいずみの存在を知り,興味をもっていただいたことによる寄稿という形である.私自身,本研究会は皆勤であるから,研究会で発表されたレポートは把握しているつもりだが,氏のようなレポート参加のみのケースは見落としていたらしい.あるいは事務局でレポートだけを印刷して研究会で配布したかもしれぬ.どちらにしろ,数学のいずみのオンライン・オフラインでの充実ぶりに事務局サイドとして感極まる思いであった(これもS先生のお陰).同時に,同じことを考える先生が全国にはいることに頭が下がり,ちょっぴり悔しくもあった.結局,アポロニウス問題についてはそのままお蔵入りとなってしまった.
それを今回,本レポートを凝りもせず寄稿したのは,小生の手詰まりによる.能力の枯渇のため原稿が遅々として進んでいないのが現状であり,だからこんなレポートでも読んでいただき,ご意見・ご感想を頂戴したいという思いなのである.
基本的に,数学教育界の長い歴史にあって,オリジナルの発想などそうそうはないと考える.今回のアポロニウスの円の問題についても研究会で発表されていなくても,黒板というレポート用紙にしっかり書かれ,生徒の目に記憶されていることは間違いないと認識している.その対象を少し,指導する教員の側に向けていただければそのアイデアがもっと整理・発展するやも知れぬ.本研究会の一理念「アイデアの相乗り」をもう一度,事務局として提案したいと考えたのである(とかっこよくいったが,行き詰った私の我がままというのが素直なところではあるが).
さて,本文についてだが,アポロニウスの円の中心のみならず,半径についても線分の両端の座標と,円の中心から求められることを示した.このことは山崎氏のレポートには触れられていないが,数研出版の方に載っていたかどうかは不明である (手元に通信33号がないため.もし掲載されていたらこのレポートはまったく意味をなさないことになるのだが).ただ,数研通信ではアポロニウスの円は,「線分を内分・外分する2点を直径の両端とする円」であることより,その中心を外分点・内分点の中点より求めているとの記載が山崎氏のレポートにあったから,ここではその軌跡が円になることも含めて証明している.その方法は,複素数平面に図形を移して求めることとした.何故複素数平面かというと,個人的に複素数でまとめるのが一番「計算の妙」があると信じているからである.図形問題を処理する道具はいろいろあろうが,計算を手際よくまとめるには複素数に勝るものはない.だが,その複素数平面も,平成16年度,3学年の受験の使い手を最後にして息絶える.残念ながら,複素数を伸縮・回転の作用素として捉えることのできる高校生はもういなくなるのである.
だから,本レポートは複素数への惜別のオマージュでもあるのだ.
 2点A,Bからの距離の比がm:n(m≠n)である点の軌跡は,ABをm2:n2に外分する点Cを中心とし,半径
2点A,Bからの距離の比がm:n(m≠n)である点の軌跡は,ABをm2:n2に外分する点Cを中心とし,半径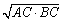 である円である.
である円である.
 2点A,Bからの距離の比がm:n(m≠n)である点の軌跡は,ABをm2:n2に外分する点Cを中心とし,半径
2点A,Bからの距離の比がm:n(m≠n)である点の軌跡は,ABをm2:n2に外分する点Cを中心とし,半径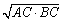 である円である.
である円である.
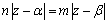 である.
である.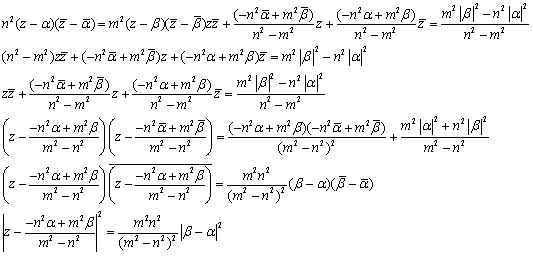
 これより,P(z)は,中心
これより,P(z)は,中心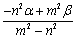 ,半径
,半径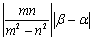 である円を表す.
である円を表す.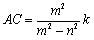 であるから,
であるから,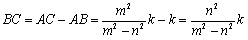
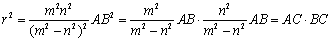
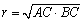 である. Q.E.D
である. Q.E.D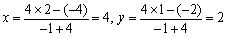
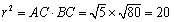 より,
より,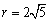
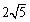 の円である.
の円である. なお,点 からアポロニュースの円に引いた直線と円との交点をP,Qとすると,方べきの定理より,
なお,点 からアポロニュースの円に引いた直線と円との交点をP,Qとすると,方べきの定理より,