Ｎｏｔｅ)

　以上、もっともらしく説明したが、この解説は不十分である。

　なぜなら、有理点に対応する友円数は、それこそ一意的ではない。

　　　
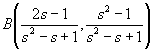
より、友円数を対応させると、
　　　
となる。よって、
　　　
なる等式を満たすs，tの値を求めなければならない。

　この値が一意的でないことは、例えば、
　　　
とすると、が得られることから分かる。

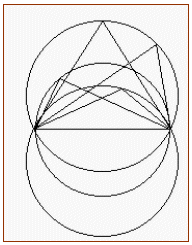　したがって、(7,5,3)のpairの友円数として、(7,5,8),(7,7,7)が見つかるが、考えてみれば、正三角形が60°の友円数になるのは当たり前である。

　確かに、k=1のときの友円数は弦の長さに対してpairとしての一意性がいえるが、それ以外のkの値に対しては、解決はしていない。

　さらに、ある弦に対する友円数は、円の大きさ（半径）も一意的でないから右図にように60°,90°，120°に対していろいろな友円数が考えられる。例えば、弦c=13に対する友円数は、
　　　(5,12,13) ………90° の友円数
　　　(8,7,13) ………60° の友円数
　　　(15,7,13) ………120°の友円数
　すなわち、k=1の場合の友円数のpairは、固定された円の弦についての一意性ということになる。

　こうやって考えていけば、結局は、何も解決していないことになる。

　だからこの一意性についてのレポートはナンセンスということになってしまうのだが、k=1の場合、曲線上の図形としての性質が実にユニークであるため、敢えて触れることにした。

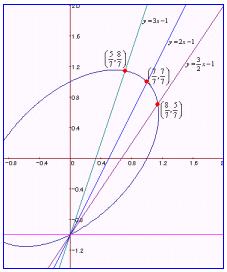　さて、一意性の問題だが、………。

　60°の友円数については、代数解析的には、右図のように２次曲線上に３組の友円数が有理点として対応していることが簡単にわかる。

　また120°についての友円数は、２次曲線上の有理点として、
　　　 の２点が対応している。

　一意性は、これ以外の有理点が果して存在するかどうかにかかっているということになる。

　さて、その解決はこのレポートをご覧になっている先生方に譲りたいと思っています。