友円数の一意性についての補足

　友円数は、弦の円周角を考えることにより補角の関係から、60°と120°の友円数のようにpairで現れることを説明した。では、このpairは一意的に確定するのであろうか。

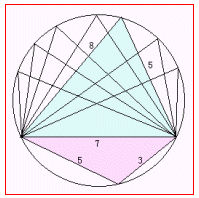　例えば、友円数 (a,b,c)=(7,5,3),(7,5,8) は弦c=7に対して決まるが、弦c=7の友円数は他にはないかということである。レポートの前半では、三角形を円に内接するように張合わせた場合、２通りの張合わせがあることを示している(その内の一つが等脚台形になる場合であるが)。この時点で一意性は崩れてはいるが、長さの関係としては、弦c=7に対して、(7,5,3)と(7,5,8)であるからその意味ではまだ一意的である。ただ、円周角により作られる無数の三角形で、辺の長さが整数であるものが存在する可能性もあるのである。

　このことをちょっと調べてみよう。

　120°に対する友円数は、楕円 x²+xy+y²=1の有理点に対応できることを前述した。

　楕円上の１点を通る直線y=tx-1と楕円の交点を求めることにより、その有理点は、
　　　
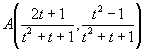
と表わされる。これから友円数の組は、(a₁，b₁，c₁)=(2t+1，t²−1，t²+t+1)となる。

　同様に、60°に対する友円数を求める。楕円x²−xy＋y²＝1と直線y＝sx−1との交点は、
　　　
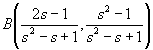
であるから、友円数の組は、(a₂，b₂，c₂)=(2s−1，s²−1，s²−s+1)である。

　ここで、c₁＝c₂のとすると、t²+t+1＝s²−s+1

　　s²−t²−s−t＝0 ，(s＋t)(s−t−1)＝0
　　辺＞０より、s>1，t>1。よって、s+t>0
　　　∴ s−t−1=0　s＝t＋1 となる。

　これを点Ｂに代入すると、
　　　
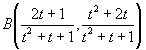
が得られる。

　よって、60°と120°の友円数のpairは、x座標が等しい２つの曲線上の有理点で与えられ、
　　(点Ａのx座標)＋(点Aのy座標)

　＝
　＝(点Ｂのy座標)
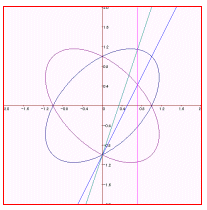
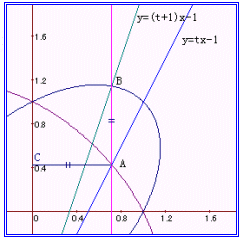
なる面白い関係が得られる。すなわち、これを２次曲線の性質とみれば、直線y＝tx−1と楕円x²＋xy＋y²＝1の交点Ａと、直線y＝(t＋1)x−1と楕円x²−xy＋y²＝1の交点Ｂのx座標は一致し、右図において、点Ａから、y軸に下ろした垂線の足をＣとすると、
　　ＡＣ＝ＡＢ
となるということである。