
![]()
1995年2月13日、フェルマーの予想が定理となった。
米プリンストン大学のアンドリュー・ワイルズ教授が、同大学の学術誌に最終定理の証明に関する論文を投稿してから4ヶ月後のことである。
一時は、「フェルマーの予想の反例が見つかった」というエイプリルフールでのメッセージが世界を駆け巡ったり、アメリカのIQ230の超天才マリリン・サバントがマスメディアを通じて「不可能」と断言してみたり、フェルマーの48もの欄外書き残しのうちの1つであるこの予想は360年間、とにかく話題に事欠くことはなかった。そして、コンピュータの解決による「四色問題」とは違った熱い感動をもって幕を閉じたのである。
しかし、それは、アマチュア数学者の夢が潰えた瞬間でもあった。πの研究と同様にどれだけ多くの自称数学者がこの問題に胸躍らせたことであろう。xn+yn=znの整数解という一見、単純かつ明解な問題に、大数学者フェルマーの予想に挑戦すべく反例をみつけようとやっきになり、惑まされそして絶望した人達は多い。多分、完全証明がなされた今でもどこかでまだ反例があると信じて研究を続けている人はいるのかもしれない。
もともと、この問題は、ピタゴラスの定理の拡張可能性についての問題であるから、やはり、ピタゴラスの定理はすごいという結論になる。どういう視点でどういう拡張が予想されるだろうと考えれば、フェルマー予想は、その1つに過ぎなく、なおかつ証明されたということは、整数解の組が見つからなかったということであり、淋しくもあるのである。整数解の組にフェルマー数と名前が冠されることは永久にない(もっともメルセンヌ数の拡張数としてのフェルマー数はあるが)。
数論の発展に大きく寄与したこの問題は素晴らしいものだけどアマチュア数学者の大半は数の神秘性に魅入られた人達で、特異な、面白い数を見つけることが楽しみなのである。別表はその一例である。
①〜③は、完全数に関するもの。友愛、社交、婚約。なんとアマチュアリズムの匂いのするネーミングであることか。
6=1+2+3, 28=1+2+4+7+14
のように、完全数は、それ自身を除く約数の和に等しい。特に最小数の6は、新プラトン学派の世界では完全を表わし、また六芒星形のように神秘的、悪魔的匂いを秘めた神の数である。その完全数がほんのちょっと姿を変えると実に人間らしい協調性を表わす数の組となる。友愛を求めて婚約したり、社交の輪を広げたりと、なんとも艶かしい数達ではないだろうか。
④〜⑥は、素数に関するもの。素数は数の元素(原子)である。その元素同士の関係も興味深いものがある。特にエマープ(emirp)数は、素数(prime)を逆さに読んだもの。洒落っ気たっぷりである。
最後に、⑦〜⑩。ピタゴラス数とその子供、孫達である。この仲間にフェルマー数は加われなかったが、どの数達も面白い性格を持っている。直角三角形の面積を考えれば、ピタゴラス数がヘロン数であるのは明らかである。
この数は、ヘロンの面積公式より、s(s-a)(s-b)(s-c),(2s=a+b+c) が平方数になるものと考えられる。3次元ピタゴラス数は、中村均先生が新川高校の生徒達と一緒に考えた数である。
a2+b2+c2=d2の整数解の存在性を先生は(n次元まで拡張させて)数学的帰納法により証明し、コンピュータプログラムによってその一部を見つけ出した。フェルマーは、「自然数は四角数であるか、あるいは2個〜4個の四角数の和で表わされる」性質を知っていたから、3次元ピタゴラス数についても強い興味を示していたのだろう。
 なお、この数の研究としては、群馬県日数教大会においても、群馬尾瀬高校の高橋先生が、「デカルト・グアの定理の関する一考察」というレポートを発表していた。
なお、この数の研究としては、群馬県日数教大会においても、群馬尾瀬高校の高橋先生が、「デカルト・グアの定理の関する一考察」というレポートを発表していた。
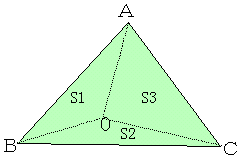
デカルト・グアの定理とは、3直角四面体OABCにおいて、
△OAB=S1,△OBC=S2,△OCA=S3,△ABC=S とするときに
S=S12+S22+S32 が成立するものである。
このレポートの中で、先生は、3次元ピタゴラス数の存在について、
S12+S22=S2−S32 と変形し、S=t+1,S3=t とおいて代入し、こうして初等整数論の手法で、3次元ピタゴラス数を求める興味あるレポートであった。S12+S22=(t+1)2−t2 =2t+1
右辺が奇数より、S1=2m,S2=2n−1とおき、代入。
(2m)2+(2n−1)2=2t+1をtに関して解いて、
t=2m2+2n2−2n 以上より、
S1=2m,S2=2n−1,S3=2m2+2n2−2n,S=2m2+2n2−2n+1
このように、ピタゴラス数の拡張の可能性はまだまだアマチュア数学者にとっては、hot themeなのである。今回の友円数についてもその1つの延長線上にある。
神々の象徴たる1,分割・誕生としての2,統合としての3,秩序としての4
数にはそれぞれの歴史とドラマがある。それが現代では、数学なる学問の計算道具としての位置付けに甘んじており、我々も、数自身の言葉に耳を傾けることはない。数は万物の根源であり、本来誰もが求めるべきものであるはずなのだが。
数達が、秋の夜の月光に張られた流星の弦がつま弾くRhapsodyにあわせて、裏返ったり、寄り添ったり、飛び跳ねたり、踊って騒ぐ光景を見ることのできる人は少ないのかもしれない。
| No |
数 名 |
組の性質 | 組の具体例 |
|---|---|---|---|
| ① | 友愛数(親和数) | それ自身を除く約数の和が相手の数になる | (284,220),(1184,1210),(2620,2924) |
| ② | 社交数 | それぞれの整数の自身を除く約数の和が数の組の次の数になり、最後の数の約数の和が最初の数になる | (103340640,123228768,124015008) |
| ③ | 婚約数 | 1とそれ自身を含まない約数の和が相手の数になる | (48,75),(140,195),(1050,1925) |
| ④ | 双子素数 | pとp+2がともに素数となる2数 | (3,5),(71,73) |
| ⑤ | 3つ子素数 | p,p+2,p+4がともに素数となる3数 | (3,5,7) のみ |
| ⑥ | エマープ数 | 互いに数字を逆から読む同じ並びになる素数 | (13,31),(107,701) |
| ⑦ | ピタゴラス数 | 直角三角形の3辺の長さで整数となるもの。 | (3,4,5),(5,12,13) |
| ⑧ | ヘロンの数 | 面積が整数となる三角形の三辺の長さ | (4,13,15),(13,14,15) |
| ⑨ | 3次元ピタゴラス数 | a2+b2+c2=d2を満たす整数解 | (1,2,2,3),(1,4,8,9) |
| ⑩ | 友円数 | 三角形の三辺の長さが整数であり、代数的に内角の1つが求まるもの | (7,5,3),(15,13,7) |