指導要領改定の目玉として、行列のピンチヒッターで登板した複素数平面は、じゃじゃ馬よろしく御し難く、あまたの騎手を鮮やかに振り落として最後には思いっきりあかんべーをして去っていこうとしている。多分、永久に。

　何がそうさせてしまったのだろう。行列も複素数も図形変換の最高のパートナーであるべきであった。行列は数学教育という社交界に颯爽とデビューし、退際も惜しまれつつプロ野球選手なら「永久に不滅です」とでいいたそうな気配であった。いまでも教科書や受験の中でその解法がファインプレーとして語り継がれている。だが、それに比べて複素数平面は、解の公式の中に辛うじて痕跡を残すのみで、多分記憶の中から忘れ去られていくのだろう。その扱い難かった解法と共に。

　確かに複素数問題は、「地味」、「ダサい」、「とろい」、イントネーションの欠如したコギャルの「〜っていうか」なる意味不明の反意語なのか何なのか知らない飾り言葉の嘲笑の真っ只中にいたような気がする。複素数本来の主張は無視され、デカルトだのベクトルだのに母屋をどかどかと土足で踏み躙られてしまった。背景も分からずx+yiとおけばいいんだよ。こんな馬鹿にされた分野もなかったかもしれない。そして次期指導要領では完全に姿を消すことになってしまったが、もう世の中はまだ4年後のことなのに誰もが次の流行分析に躍起になり、複素数平面なんてまだあったの。それでも複素数は解法に意地張っているもんだから余計哀愁を誘ってしまう。

　複素数はそりゃ行列のように最新ファッションじゃない。レトロ趣味と言われてしまえばそれまでである。でも古くて新しい学問でもある。複素数の概念が、電気や力といった物理学分野の現代化に果たした功績は大きい。 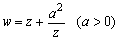　 の軌跡についての問題は意味も分からずよく出題されるが、実はきちっとした名前がある。Joucowski変換。流体力学では知らぬ者はいない。かっこいいじゃないか。でも教育数学では、zが単位円であるときの軌跡は楕円であることの計算練習にしか評価されていない。一見するとチョーダサいのに実はエレガントだったりもするのだ。そして、その典型的なものが一次分数関数だったような気がする。

　一次分数関数、別名一次変換。行列で表現できるからまた複素数は出鼻を挫かれてしまったが、この変換の中で唯一複素数が譲らなかったものがある。それが鏡像変換である。幾何でいう反転だが、そうみれば結局幾何の分野で解決できるのじゃないかということになるがけっしてそうではない。むしろ幾何の星の数ほどある定理の大半は複素数平面で解決できてしまう。反転もその一つに過ぎない。ところがこの反転の概念が残念ながら高校現場では生かせなかった。

　　　f：z　→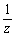　

　この変換が他の変換に比べて厄介過ぎるのだ。懐深い複素数の牙城の前に誰もが屈し、唾を吐き捨て他の道を選択してしまった。なぜこの道は険しかったか。それは無限への旅であるからである。

　このレポートの表題は「メービウスのわだち」である。メービウス(M?bius)とはもちろんあの「メービウスの帯」の考案者のことである。リボンの両端を掴んで一ひねり(二ひねりでもいいが)してつなぎ合わせると摩訶不思議な世界か生まれる。一面を辿っていくといつの間にか出発点に戻ってしまう。メービウスは裏表のない世界なのだ。この興味をそそる奇妙さを人々はほって置くはずもなく、妙な宗教の象徴に祭り上げられたり、アフガンバンドと名を変え、奇術の世界で脚光を浴びたりしている。

　で、実はこのメービウスの名を冠しているのが、 f：z　→　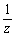 なのである。この変換をメービウス変換という。

　メービウスはその帯の影に隠れてしまい、優れた数学者であったということは意外と知られていない。大体、メービウスが活躍した19世紀初頭は怪物が多すぎた。ガロア、アーベル、ブール、コーシー、ロバチェフスキー、ヤコービ、ハミルトン、ケーリー、ワイエルストラス、なんでこんなにいっぱいいるんだ。そうそう、あのガウスおじいさんもまだ健在であった。射影幾何学の完成者、トポロジーへのパイオニアとまでいわれた彼も、こんな怪物たちの前では確かに影は薄かったかもしれない。でも彼の功績はメービウス幾何学として確実に完成していくのである。

　さて、メービウス変換に話を戻そう。この変換、すなわち反転の面白いことは、無限がゼロに繋がるということである。

　　　　　OP・OQ=1

　わずかこれだけの式の中に無限の定義がある。「猿の惑星」、「青い鳥」(メーテルリンク)のように、旅の果てが出発点だったりするのはよくある現実。そんな現実がまさにメービウスの輪なのである。だがそれは高校数学が という値に、不可侵の呪文をかけ、禁断の言葉としてしまつたことにより踏み込めなくなってしまった世界でもあるのだ。架空と現実。そのバランスもまたメービウスは弄んでいた。そう考えると確かにメービウス変換は恣意的ではあるが我々の侵入を拒んでいたような気もする。いみじくもメービウスはこういった。

数学においても音楽や絵画や詩の場合と同じことである。だれでも思慮分別があり勉強が好きならば、法律家や医者や科学者にはなることができるし、それぞれの分野で成功をおさめることができる。しかし数学者にはだれでもなれるものではない。ふつう程度の思慮分別や勉強好きでは、この場合、何の意味もないのである。

　なんて強烈な言葉であろう。我々は彼によって新世界への扉を開くことを拒絶されてしまった。チョー軽い何の意味もない高校生にとっては何の意味もない言葉かもしれないが、「無限に遊ぶ」楽しみが高校数学からネバーエンディングストーリーのファンタージェンの世界のように淡く実体が薄れてきているのであるとしたら、我々が数学を学ぶ意味がそのうち本当に何の意味もなくなってしまうのかもしれない。

　後年、ライプニッツ天文台の天文台長の職に就いた彼は、満天の夜の星の瞬きに、どんな夢をみていたのだろうか。

※このメービウスの帯が織成す世界を稲雲高校の大河内先生は、ヒルベルト空間なんかと比較してファンタジー空間と命名しました。このメービウス変換もコンピュータグラフィックで再現するとさぞや美しい模様が描けるかと思います。それは多分、藻岩高校と稲北高校のどちらかのM．S先生がやってくれると信じています。