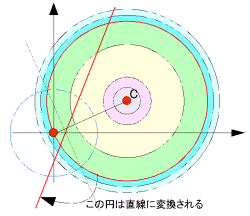
f:z →
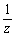
である反転について調べればよいことになる。
 Chap.9では、「弦は弦に移されるが、線分という意味ではない」とか、「円の中心は円の中心には移されない」というような曖昧な表現をしてきたが、このことからも必ずしも内部から内部に移されるわけではないことが予想されよう。実際、変換fは非線形である。
Chap.9では、「弦は弦に移されるが、線分という意味ではない」とか、「円の中心は円の中心には移されない」というような曖昧な表現をしてきたが、このことからも必ずしも内部から内部に移されるわけではないことが予想されよう。実際、変換fは非線形である。
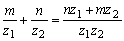 から明らかである。よって、線分は線分に移されないことになる。円が円に移されないことは前述した。
から明らかである。よって、線分は線分に移されないことになる。円が円に移されないことは前述した。
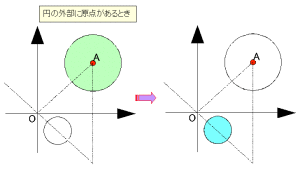
例えば、原点が円の内部にある場合について考えてみよう。
中心C(α)、半径rの円はfにより円に移されるが、中心Cの同心円を考えて半径を縮めていくと、r=|α|のとき円は原点を通る。このとき、円はfにより直線に変換される。このとき変換像は有界でなくなるため、円の内部に移れないことになってしまう。
すなわちベキの値 λ=|α|2-r2 が円の内部変換な関わりをもっていることになる。
λの値を変化させて調べてみよう。
λ>0のとき、原点は円の外部にある。原点から円に引いた接線の接点をTとおくと、λ=OT2であり、|α|>OTとなる。ここで、r→0とすると、OT→|α|
よって、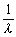 の値は減少するからfにより円の内部に円が作られ埋め尽くされることになる。
の値は減少するからfにより円の内部に円が作られ埋め尽くされることになる。
λ<0のとき、|α|<rであるから原点は円の内部にある。
r→|α|とすると、λ → 0 であるから変換像である円の半径は 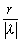 →∞となり、直線に近似していく。更にrの値をr>|α|となるように増加させると、円の半径は縮小し、点
→∞となり、直線に近似していく。更にrの値をr>|α|となるように増加させると、円の半径は縮小し、点 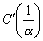 に収束する。すなわち、円Cの内部は円C´の外部に変換されることが予想される。
に収束する。すなわち、円Cの内部は円C´の外部に変換されることが予想される。
以下、そのことを示す。
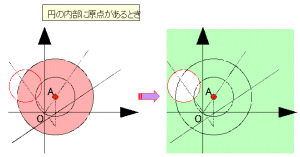 半径rで中心A(α)の円をCとし、f:z → w により変換された円をC´とする。円Cの周および内部を表す式は、
半径rで中心A(α)の円をCとし、f:z → w により変換された円をC´とする。円Cの周および内部を表す式は、
|z-α|≦r
である。 を代入して整理すると
|αw-1|≦r|w|
両辺を平方して
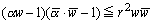
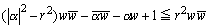
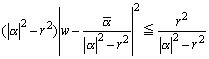
 ここで、λ=|α|2-r2 とおくと、
ここで、λ=|α|2-r2 とおくと、
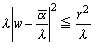
すなわち、
λ>0のとき、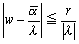 より円C´の周および内部に移る。
より円C´の周および内部に移る。
λ<0のとき、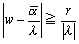 より円C´の周および外部に移る。
より円C´の周および外部に移る。
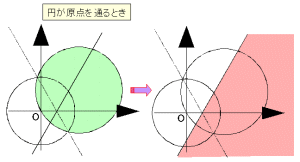 なお、r=|α|のときは、円Cは直線に移されるが、周および内部はどうなるだろうか。
なお、r=|α|のときは、円Cは直線に移されるが、周および内部はどうなるだろうか。
|z-α|≦|α| に z=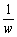 を代入して整理すると、
を代入して整理すると、
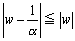
これは、点A(α)の反転をA´とするとき、A´P´≦OP´を満たす点であるから、OA´の垂直二等分lの直線上およびlを境界線とする領域で原点を含まない側を表している。
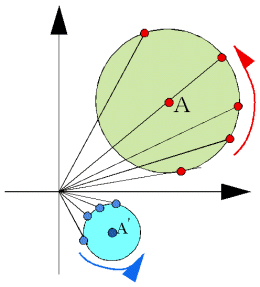
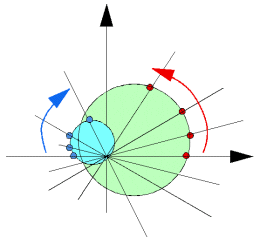
ところで、円C上の点を円の中心に対して反時計回りに回転させ、一回りしたところで円の半径を僅かだけ縮め同様に回転させていくとすると、反転の像にどのように点を移されていくだろうか。
これは共役反転の意味を考えると分かる。円の外部に原点があるとき、ベキ>0であるから、点は実軸に対称に移動したあと、正の値で伸縮される。これに対して原点が円の内部にあるとき、ベキ<0であるから、実軸対称のあと、負の伸縮、すなわち原点に対して対称な象限に点は移される。
以上のことより、原点が円の外部にあるとき、同様に反時計回りに内側に渦を描く。原点が円の内部にあるとき、時計回りに外側に渦が無限の彼方に広がっていくのである。