f : Z →
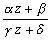
は平行移動、相似、共役反転の合成変換であり、一次分数関数を分解して順次視覚的に変換をしていけばいいことが分かった。
実際に幾つかの例題でこのことを確認する。
《演 習》
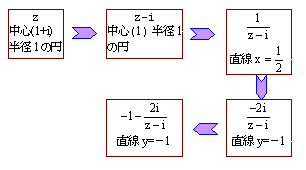
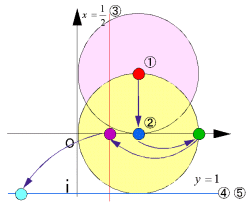
Ex) zは複素数平面で、点1+iを中心とする半径1の円周上を動くとき、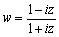 で表される点wの軌跡を求めよ。 (小樽商科大学) |
解)
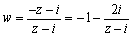 である。
である。ここで、z-i は中心1半径1の円より原点を通る。
従って、
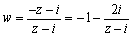 は直線に変換される。原点と円 z-i との最大距離点は2より直線の方程式は
は直線に変換される。原点と円 z-i との最大距離点は2より直線の方程式は 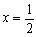
ex) |z|=1 のとき、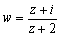 の軌跡を求めよ。 の軌跡を求めよ。
|
まず、一般的な解法から試みよう。
解1)
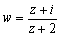 より
よりwz+2w=z+i z(w-1)=-2w+i
両辺の大きさをとって、
|z(w-1)|=|-2w+i| ∴ |z||w-1|=|2w-i|
|z|=1より
|w-1|=|2w-i|
両辺を平方して
|w-1|2=|2w-i|2
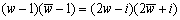
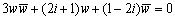
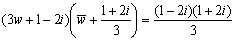
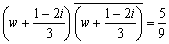
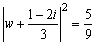
∴
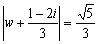
よって、中心
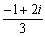 で半径
で半径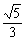 の円。
の円。
解2)
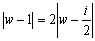
A(1),
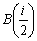 とすると、(*)を満たす点P(w)の軌跡は、AP=2BPより、
とすると、(*)を満たす点P(w)の軌跡は、AP=2BPより、AP:BP=2:1
よって、点Pは線分ABを 2:1 の比に内分する点をQ外分する点Rとするとき、線分QRを直径の両端とする円(アポロニュースの円)である。
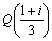 ,
, 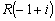 であるから、
であるから、円の中心はQRの中点
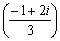 であり、QR=
であり、QR=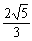 より半径は
より半径は 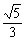 である。
である。
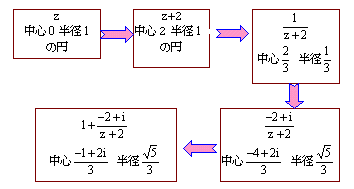
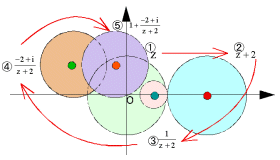
解3)
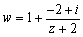 より、
より、z+2は、中心2で半径1の円だから原点は通らない。
したがって円は円に移される。
ベキの値は、λ=1×3=3