|
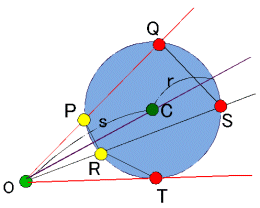
暯柺忋偺揰O偐傜掕墌偵堷偄偨俀杮偺慄暘偑丄墌偲偦傟偧傟俀揰偱岎傢傞偲偒丄偦偺岎揰傪偦傟偧傟P,Q,R,S偲偡傟偽丄師幃偑惉棫偡傞丅 丂丂丂丂OP丒OQ=OR丒OS |
 徹柧)
徹柧)
傛偭偰丄OP丗OR=OS丗OQ
偙傟偐傜丄OP丒OQ=OR丒OS傪摼傞丅
丂墌偺拞怱C偵懳偟丄OC=s丄墌偺敿宎r偲偡傞偲丄
丂丂丂OP丒OQ=OR丒OS =(s-r)(s+r)=s2-r2
丂傑偨丄慄暘偺堦曽偑墌偵愙偡傞偲偒丄
丂丂丂OP丒OQ=OR丒OS = s2-r2=OT2
偱偁傝丄偦偺愊偼忢偵堦掕抣偲側傞丅偙偺抣傪儀僉偲偄偆丅
 側偍丄偙偺曽儀僉偺掕棟偵偍偗傞慄暘偼桳岦慄暘偱偁傞丅
側偍丄偙偺曽儀僉偺掕棟偵偍偗傞慄暘偼桳岦慄暘偱偁傞丅
丂丂丂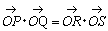
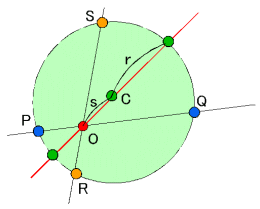
偲峫偊傞偲丄揰O偑墌偺撪晹偵偁傞応崌偵偍偄偰傕曽儀僉偺掕棟偼惉棫偡傞丅
丂丂丂OP丒OQ=OR丒OS =(s-r)(s+r)= s2- r2<0
偡側傢偪丄揰O偑墌偺奜晹偺応崌偼丄OP丒OQ>0,墌偺撪晹偺応崌偼丄OP丒OQ<0偲側傞傢偗偱偁傞丅
丂偙偺儀僉偺抣偑嫟栶斀揮曄姺偵偳偺傛偆偵娭傢偭偰偔傞偐傒偰傒傛偆丅
|
墌廃忋偺尫PQ傑偨偼偦偺墑挿偑尨揰傪捠傞偲偡傞丅 f丗z丂仺丂 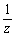 偵偍偄偰丄墌偑墌偵堏偝傟丄P丩=f(P) ,Q丩=f(Q) 側傜偽丄尫P丩Q丩偺挿偝偼丄尫PQ偺挿偝偵斾椺偡傞丅 偵偍偄偰丄墌偑墌偵堏偝傟丄P丩=f(P) ,Q丩=f(Q) 側傜偽丄尫P丩Q丩偺挿偝偼丄尫PQ偺挿偝偵斾椺偡傞丅
|
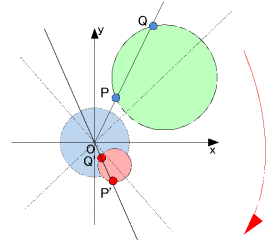 拞怱A(兛)丄敿宎r偺墌廃忋偺俀揰傪P(z1),Q(z2)偲偟丄偦傟偧傟偺f偵傛傞憸傪
P丩(z1丩),Q丩(z2丩) 偲偡傞丅偙偺偲偒柧傜偐偵捈慄 P丩Q丩 偼尨揰傪捠傞丅傑偨丄
拞怱A(兛)丄敿宎r偺墌廃忋偺俀揰傪P(z1),Q(z2)偲偟丄偦傟偧傟偺f偵傛傞憸傪
P丩(z1丩),Q丩(z2丩) 偲偡傞丅偙偺偲偒柧傜偐偵捈慄 P丩Q丩 偼尨揰傪捠傞丅傑偨丄
丂丂丂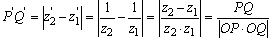
丂偙偙偱丄曽傋偒偺掕棟傛傝丄OP丒OQ=兩(傋偒)偲偡傞偲丄
丂丂丂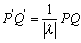
丂傛偭偰丄墌偑墌偵堏偝傟傞偲偒丄懳墳偡傞尨揰傪捠傞尫偺挿偝偼丄斾椺偡傞偙偲偑暘偐傞丅
丂偙傟偐傜嵟戝尫偱偁傞墌偺捈宎偼傑偨捈宎偵堏偝傟傞偲偄偆偙偲偑傢偐傞乮偨偩偟丄捈宎偺椉抂偑捈宎偺椉抂偵堏偝傟傞偲偄偆偩偗偱偁傝丄慄暘偑堏偝傟傞偲偄偆偙偲偱偼側偄乯丅
f丗z丂仺丂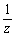 偵傛傝丄墌C偑墌C丩偵堏偝傟傞偲偒丄 偵傛傝丄墌C偑墌C丩偵堏偝傟傞偲偒丄慄暘傑偨偼偦偺墑挿忋偵尨揰偑偁傞墌C偺捈宎偼墌C丩偺捈宎偵堏偝傟傞丅 |
丂側偍丄捈宎偩偗偺曄姺偱偁傟偽師偺傛偆偵峫偊傞偙偲傕壜擻偱偁傞丅
丂墌C忋偺捈宎傪A(z1), B(z2)偲偟丄A,B埲奜偺墌廃忋偺揰傪P(z)偲偡傞丅曄姺f偺憸傪偦傟偧傟丄A丩(w1),B丩(w2),P丩(w)偲偡傟偽丄
丂丂丂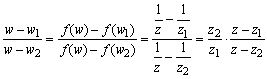 丂偙偙偱丄佢APB=90亱偱偁傞偐傜
丂偙偙偱丄佢APB=90亱偱偁傞偐傜 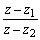 偼弮嫊悢丅傑偨丄嶰揰O,A,B偑堦捈慄忋偵偁傞偲偒丄
偼弮嫊悢丅傑偨丄嶰揰O,A,B偑堦捈慄忋偵偁傞偲偒丄 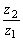 偼幚悢偱偁傞偐傜丄
偼幚悢偱偁傞偐傜丄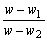 偼弮嫊悢偱偁傞丅傛偭偰丄佢A丩P丩B丩=90亱 偲側傝丄A丩B丩偼捈宎偲側傞丅
偼弮嫊悢偱偁傞丅傛偭偰丄佢A丩P丩B丩=90亱 偲側傝丄A丩B丩偼捈宎偲側傞丅
f丗z丂仺丂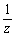 偵傛傝丄墌C偑墌C丩偵堏偝傟傞偲偡傞丅 偵傛傝丄墌C偑墌C丩偵堏偝傟傞偲偡傞丅墌C偺尨揰O偵懳偡傞儀僉偑兩偱偁傞偲偒丄墌C丩偺O偵懳偡傞儀僉偼 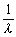 偱偁傞丅 偱偁傞丅
|
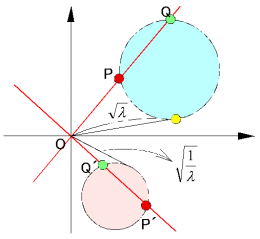 徹柧
徹柧
丂丂丂OP丒OP丩=1,丂OQ丒OQ丩=1 乧乧(*) 傑偨丄墌C偵偍偄偰曽儀僉偺掕棟傛傝丄
丂丂丂OPQ=兩(儀僉)
(*)偺擇幃傪曈乆偐偗傞偲
丂丂丂OP丒OP丩丒OQ丒OQ丩= 1
丂丂丂亪丂
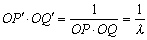
丂尨揰傪捠傞捈慄偼丄尨揰傪捠傞捈慄偵堏偝傟傞偐傜尨揰傪捠傞墌俠偺尫偼丄尨揰傪捠傞墌俠丩偺尫偵堏偝傟傞丅
丂傛偭偰丄O,P丩,Q丩偼堦捈慄忋偵偁傞偐傜 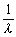 偑儀僉偺抣偱偁傞丅
偑儀僉偺抣偱偁傞丅
丂埲忋偺偙偲傛傝師偺寢壥傪摼傞丅
f丗z丂仺丂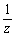 偵傛傝丄拞怱A(兛),敿宎r偺墌C偑墌C`偵堏偝傟傞偲偒丄 偵傛傝丄拞怱A(兛),敿宎r偺墌C偑墌C`偵堏偝傟傞偲偒丄丂丂嘆墌 偺敿宎偼 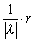 丂丂嘇墌 偺拞怱偼 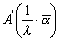 偱偁傞丅偨偩偟丄兩偼丄墌C偺尨揰偵懳偡傞儀僉偺抣偱偁傞丅 |
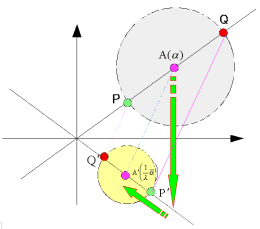 嘆偼柧傜偐偱偁傞丅
嘆偼柧傜偐偱偁傞丅
傑偨丄尨揰偲墌C偺拞怱A傪捠傞捈慄偼丄f偵傛傞幚幉偵娭偟偰懳徧側捈慄偵曄姺偝傟傞丅傛偭偰偦偺忋偵偁傞捈宎傕摨條偵曄姺偝傟傞丅偙偺偙偲傛傝丄墌C丩偺拞怱傕傑偨偦偺捈慄忋偵偁傞偙偲偵側傞丅傛偭偰丄揰A偺幚幉懳徧揰偲尨揰傪寢傇捈慄忋偵拞怱偼偁傞丅偦偟偰丄儀僉偺抣偑 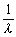 偱偁傞偙偲傛傝嘇偑摼傜傟傞丅
偱偁傞偙偲傛傝嘇偑摼傜傟傞丅
丂側偍丄墌偺拞怱偼墌偺拞怱偵堏傞傢偗偱偼側偄丅幚嵺
丂丂丂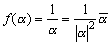
偱偁傞偑丄
丂丂丂兩=|兛|2
偲側傞偙偲偼側偄丅
|
墌C偑尨揰O傪捠傞偲偒丄 f丗z丂仺丂 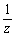 偵傛偭偰丄墌廃忋偺揰P(z)偼丄尨揰O偲墌C偺拞怱傪寢傇捈宎偺O埲奜偺抂揰B偺斀揮B丩傪捠傝OB丩偵悅捈側捈慄偵曄姺偝傟傞丅 偵傛偭偰丄墌廃忋偺揰P(z)偼丄尨揰O偲墌C偺拞怱傪寢傇捈宎偺O埲奜偺抂揰B偺斀揮B丩傪捠傝OB丩偵悅捈側捈慄偵曄姺偝傟傞丅
|
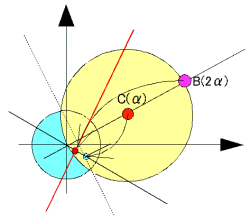 丂尨揰偼丄斀揮偵傛傝柍尷墦揰偵懳墳偡傞丅
丂尨揰偼丄斀揮偵傛傝柍尷墦揰偵懳墳偡傞丅
傑偨丄尨揰偐傜傕偭偲傕棧傟偨揰偼傕偭偲傕嫍棧偺抁偄揰偲側傞丅
傛偭偰恾偺捈宎偺抂揰B偑墌廃忋偺尨揰偐傜偺嵟戝嫍棧偺揰偱偁傞偐傜丄偙偺斀揮B丩偑嵟抁揰偱偁傞丅偦偟偰媮傔傞恾宍偼捈慄偱偁傞偐傜丄揰B丩偼尨揰偐傜媮傔傞捈慄偵壓傠偟偨悅慄偺懌偲偄偆偙偲偵側傞丅娙扨偵偄偊偽丄墌偺拞怱C偺斀揮傪C丩偲偡傞偲丄OC丩偺悅捈偵摍暘慄偱偁傞丅
丂側偍丄尨揰傪捠傞墌偑扨埵墌偲岎傢傞偲偒丄偦偺岎揰偺斀揮偼丄幚幉懳徧揰偵側傞偐傜偦偺嬀憸偱偁傞2揰傪捠傞捈慄偑憸偱偁傞丅
|
墌C偑尨揰O傪捠傝扨埵墌偲岎傢傞偲偒丄 f丗z丂仺丂 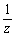 偵傛偭偰丄墌廃忋偺揰P(z)偼丄墌C偲扨埵墌偲偺2岎揰傪捠傞捈慄傪幚幉懳徧堏摦偟偨捈慄偵曄姺偝傟傞丅 偵傛偭偰丄墌廃忋偺揰P(z)偼丄墌C偲扨埵墌偲偺2岎揰傪捠傞捈慄傪幚幉懳徧堏摦偟偨捈慄偵曄姺偝傟傞丅
|
|
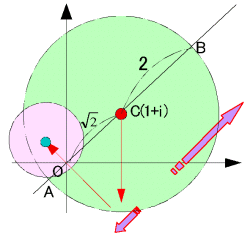
ex) 揰P(z)偑師偺墌廃忋偺揰偱偁傞偲偒丄 丂丂丂f丗z丂仺丂  偱堏偝傟傞揰Q(w)偺婳愓傪媮傔傛丅 丂(1) 敿宎2偱拞怱A(2)偱偁傞墌C 丂(2) 敿宎1偱拞怱3+4i偱偁傞墌 丂(3) 敿宎2偱拞怱1+i偱偁傞墌 |
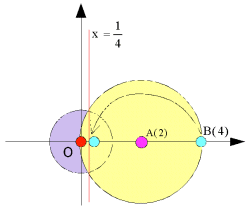 (1)偺夝)
(1)偺夝)
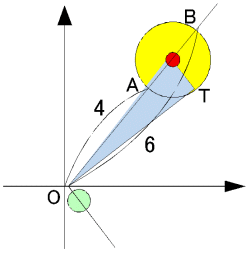
尨揰偐傜傕偭偲傕棧傟偨墌廃忋偺揰偼丄B(4)偱偁傞丅
偦偺嬀憸偼
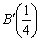 偱偁傞偐傜丄
偱偁傞偐傜丄丂丂丂OB丩偵悅捈側捈慄
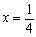
偵堏偝傟傞丅
 (2)偺夝)
(2)偺夝)
墌C偺拞怱偲尨揰O傪捠傞捈慄偲墌C偲偺岎揰傪A,B偲偡傞偲丄尨揰偲墌C偺拞怱C(3+4i)偲偺嫍棧偼OC=5偱偁傞偐傜丄兩=OA丒OB=4亊6=24 (偁傞偄偼丄OT2=OC2-CT2=25-1=24)
丂傛偭偰媮傔傞墌偺拞怱偼 丄
丂丂丂
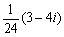
傑偨敿宎偼丄
丂丂丂
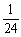
偱偁傞丅
 (俁)偺夝)
(俁)偺夝)
尨揰O偲墌偺拞怱C偲偺嫍棧偼丄
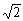 偱偁傞偐傜丄
偱偁傞偐傜丄丂丂丂
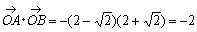
傛偭偰丄墌C偺憸墌C丩偺拞怱偼丄
丂丂丂
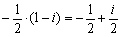
傑偨丄敿宎偼
丂丂丂
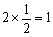
偱偁傞丅
Remark)
(1)乣(3)偺捠忢偺夝摎偼師偺傛偆偵側傞丅
偦傟偧傟偺墌傪幃偱昞尰偡傞偲丄
丂(1) |z-2|=2 (2) |z-(3+4i)|=1 (3) |z-(1+i)|=2
偙偙偱丄z=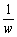 傪戙擖偟偰奺幃傪惍棟偡傞偲丄
傪戙擖偟偰奺幃傪惍棟偡傞偲丄
(1) 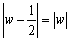 傛傝丄擇揰(0),
傛傝丄擇揰(0), 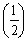 偐傜摍嫍棧偵偁傞婳愓丅偡側傢偪捈慄
偐傜摍嫍棧偵偁傞婳愓丅偡側傢偪捈慄 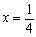
(2) 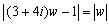 傛傝
傛傝 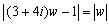
丂傛偭偰丄擇揰(0), 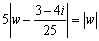 傪寢傇慄暘傪5丗1偺斾偵撪暘丄奜暘偡傞揰傪捈宎偺椉抂偲偡傞墌丅
傪寢傇慄暘傪5丗1偺斾偵撪暘丄奜暘偡傞揰傪捈宎偺椉抂偲偡傞墌丅
(3) 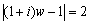 丂
丂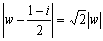
丂傛偭偰丄擇揰(0),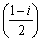 傪寢傇慄暘傪 1丗
傪寢傇慄暘傪 1丗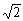 偺斾偵撪暘丄奜暘偡傞揰傪捈宎偺椉抂偲偡傞墌丅
偺斾偵撪暘丄奜暘偡傞揰傪捈宎偺椉抂偲偡傞墌丅