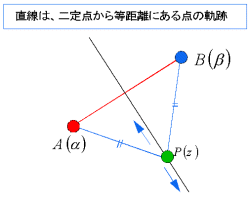複素数平面上の異なる２点A(α),B(β)に対して、
　　　　　AP=BP
を満たす点P(z)は、線分ABの垂直二等分線を表す。これから直線の方程式は、
　　　　|z-α|=|z-β|
　　　　∴　
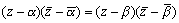
　これを整理して、λ=α-β,D=|α|²-|β|² (λ∈C, D∈R) とおくと、
　　　　
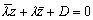
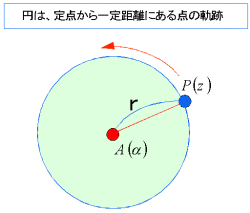
　また、点A(α)を中心とする半径rの円周上の点P(z)は、
　　　　|z-α|=r
　これより、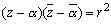
　　　　∴　
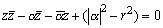
λ=-α, D=|α|²-r² (λ∈C, D∈R)とおくと、
　　　　

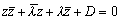
　以上より、直線または円の方程式は、
　　　
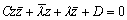
で与えられることがわかる。

　このとき、f：z　→　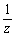 なる変換の像wは、z= 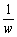であるから代入して、
　　　
　　　
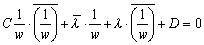
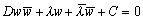
D=0のとき直線を表し、D≠0のとき円を表す。よって複素数平面上の円または直線は、円または直線に移されることが分かる。

　以上より、一次変換
　　　f：z　→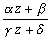　
により、直線を広義の円と考えると、円は円に移される。

　この対応を円々対応という。