z=αz1+β (α,β∈C)
と表される。この円P(z)のf:z →
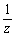 による変換像Q(w)を求めてみよう。
による変換像Q(w)を求めてみよう。
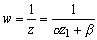 より、w(αz1+β)=1
より、w(αz1+β)=1
wαz1+wβ=1
αwz1=1-wβ
|α||w||z1|=|wβ-1|
|z1|=1より、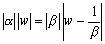 ………(*)
………(*)
(*)は、|α|=|β|のとき、原点Oと中心Cの反点C´を結ぶ線分OC´の垂直二等分線を表す。このとき、zは原点を通る円である。
|α|≠|β|のときは、線分OC´を|β|:|α|の比に内分および外分する2点を直径の両端とする円を表す。
|
(1) 原点を通る円は直線に移される。 (2) 原点を通らない円は円に移される。 |
ではzの軌跡が円に移されるとき、円の中心と半径を次に求める。
(*)の両辺を平方して、
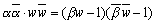
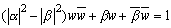
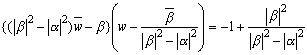
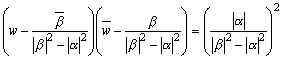
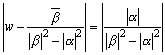
よって、中心 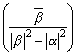 で半径
で半径 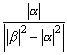 の円となる。
の円となる。
f:z → 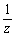 なる共役反転変換により、中心C(β),半径|α|の円は なる共役反転変換により、中心C(β),半径|α|の円は○D=0のとき、円は直線に移される。 ○D≠0のとき、円は円に移される。ただし、D=|β|2-|α|2 である。 |