 複素数平面上の原点を通る直線は、z=teiθ (t∈R) と表される。
複素数平面上の原点を通る直線は、z=teiθ (t∈R) と表される。したがって、
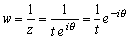
による像もまた原点を通る直線である。
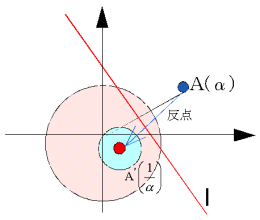
次に、原点を通らない直線lの像を求めてみよう。
l 上の点P(z)は、l に関して原点Oと対称な点をA(α)とすると、
|z-α|=|z|
を満たす(線分OAの垂直二等分線が l である)。
w=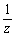 のとき、z=
のとき、z=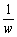 より、
より、
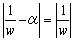
∴ |1-αw|=1
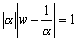
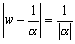
∴ wは点 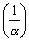 を中心とする原点を通る円周上の点である。
を中心とする原点を通る円周上の点である。
以上より次の結論を得る。
f:z → 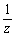 なる共役反転変換により、 なる共役反転変換により、○原点を通る直線は実軸に対称な直線に移される。 ○原点を通らない直線は、原点に関して直線と対称な点をαとすると、f(α)を中心とする原点を通る円に移される。 |
リーマン球面における無限遠点の定義より、原点Oの反転は∞であり、∞の反転は原点である。これから原点を通らない直線上の無限遠点(二点)は原点に変換される。また、原点からの距離が最小である直線上の点(原点から直線に下ろした垂線の足H)は、最大距離点に移される。すなわち点OAの中点 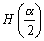 の像を
の像を 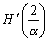 とすると、OH´は像である円の直径を表すことになる。
とすると、OH´は像である円の直径を表すことになる。
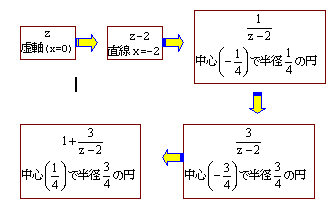
ex) 複素数zに対して、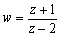 とおく。 とおく。複素数平面上で、複素数zを表す点が虚軸上を動くとき、複素数wを表す点はどんな図形を描くか。
(長崎総合科学大)
|
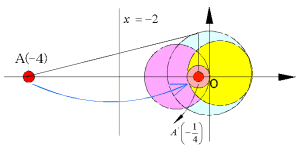
解) 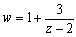 より、直線x=-2に対して、原点との対称点A(-4)の反転を考えると、次のようになる。
より、直線x=-2に対して、原点との対称点A(-4)の反転を考えると、次のようになる。