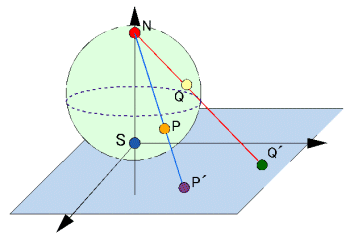
f：z →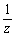 
なる一次変換は、複素数平面C上の点をリーマン球面上の点に対応させることにより、z=0を含めて１対１対応が可能となる。複素数平面Cの原点に右図のように直径をSNとする接球面をのせる。このとき、N極を通る直線が球面とおよび複素数平面と交わる点をそれぞれP,P´とするとPとP´は1対1対応となる。
P → N
とするとき、Pは複素数平面上の無限遠点∞に対応する。こうすることにより、リーマン球面と複素数平面は同相となる。
すなわち、z=0のとき、w=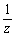により、w=∞とみるわけである。