@Decimal BASIC has a show feature, "the picture definition".
@By describing the figure data beforehand as the deputy program, it is possible to transform such as the parallel displacement, the extension, contraction, the turn, and shear. We can think these transformation changes which the complex number as operator has. Therefore, Decimal BASIC has made possible even the change of the set in addition to the point.
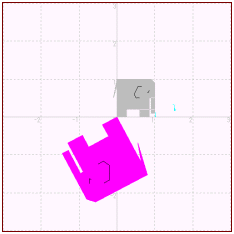
@prog2 is the program to show the image (the image of the elephant) after the change in taking advantage of the complex number at the elephant (the unit elephant) which was made a square with one piece of length as the big frame.
prog2 ! The exponentiation change of unit elephant picture elephant ! The picture definition of the unit elephant set area color col plot area:0,0;0.25,0;0.25,0.2;0.6,0.2;0.6,0;0.85,0;0.85,0.5; & & 0.9,0.5; 0.9,0.1;1,0.1;1,0.9;0.9,1;0,1;-0.1,0.5;0,0.8;0,0 ! The body of the elephant plot lines:0.65,0.8;0.55,0.8;0.45,0.6;0.5,0.5;0.6,0.506 ! The ear of the elephant plot lines:0.85,0.7;0.82,0.64;0.79,0.66; ! The eye of the elephant end picture set window -4,4,-4,4 option angle degrees draw grid let col=2 draw elephant input prompt "a,b=":a,b let r1=sqr(a^2+b^2) ! The absolute value let c1=angle(a,b) ! The Argument if r1>1 then let s=0.02 else let s=-0.02 end if if c1<0 then let c1=360+c1 end if for r=1 to r1 step s ! The zooming display set draw mode hidden let col=0 draw elephant with scale(r-s) draw grid let col=5 draw elephant with scale(r) set draw mode explicit next r for c=0 to c1 step 1 ! The turn set draw mode hidden let col=0 draw elephant with scale(r)*rotate (c-1) draw grid let col=7 draw elephant with scale(r)*rotate(c) set draw mode explicit next c LET col=15 draw elephant END |
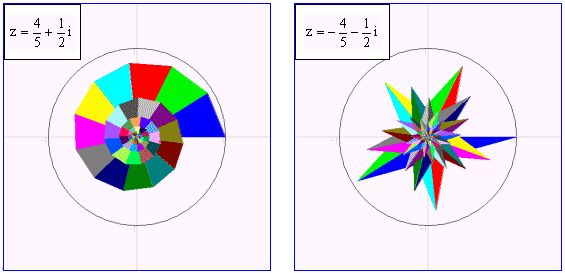
@It computes the size and the argument of the complex number, uses "for next" direction, and transforms a diagram as the animation in order of the elasticity, the turn. There is a way of moving a diagram variously, but here, it takes the technique to rewrite again in the background color to erase an afterimage ( the elephant ).
@ "set draw mode hidden", "explicit" are the personal special processing of Decimal BASIC which suppresses flickering in case of animation in the direction which draws a figure with the bit map memory, the direction to make it reflect in the screen respectively.
@prog2 actually is a program which replaced the one created about 10 years ago in N88BASIC as a supplementary teaching aid of linear transformation in the matrix. In N88BASIC, by using the "line" direction, the formula of linear transformation had to be written in each of the segments, which eventually made the program very long with a great number of lines. Decimal BASIC gets rid of the pain of writing such a long program.
@In the above-mentioned two programs, actually, you make complex number x+yi correspond to point (x,y) on the Cartesian coordinates and picture the track only. Therefore, the program doesn't show the nature of the complex number and it is displaying the result of the nature only.
@In conventional BASIC, this was a limit. However, in Decimal BASIC, the mode to express in the complex number except handling the numerical value as the decimal number is prepared. In this mode, the output of the complex number is shown in the brackets as a pair in the real part and the imaginary part. An imaginary number unit i can be handled by the following line:
@@@let i=sqr(-1)@( or, it is let i=complex(0,1) ),
@The use of the complex number mode expands the use of the complex plane unit mainly in high school mathematics B.
@prog3 is the program to output the size, the argument, and the square number of the input complex number. The development of synthetic skills in students can be attempted by analyzing a problem and experimenting with a program, and not only showing an output.
prog3 ! Computation of the complex number OPTION ARITHMETIC COMPLEX OPTION ANGLE DEGREES input prompt "a,b=": a,b let z=complex(a,b) print "z=";re(z);"+";im(z);"i" print "|z|=";abs(z) print "arg(z)=:";arg(z) print "z^2=";re(z^2);"+";im(z^2);"i" END |
@For example, in (prog1), it sets a complex number mode and rewrites the main part of the show of the syntax "for next" as follows,
@@@plot area:0,0;re(z^n),im(z^n);re(z^n1),im(z^n1)
@The show by involution is executed in the gauss plane. When you compare agreement of the difference and the output of the program of both, the nature of the complex numbers such as the theorem of De Moivre is understood.
@In the following section, frequency problems in mathematics B will be analyzed by Decimal BASIC.
@
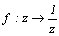is called moubius change, the guide of this change becomes difficult in the high school scene of the complex number change. It finds that w is an elastic number to 
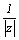in the together conjugate complex number 
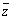from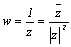 
. This relation 
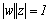is the reflection in the geometry. Therefore, it is possible to think that moubius change is the reflection change of the conjugate complex number.
@To unit circle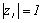 
on the complex plane, the circle with the radius 1 which center is Ώ is expressed like 
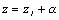. Let's try to find the locus of the point 
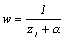which changed point z on this circumference in moubius.
@prog4 is the program which shows in the locus. It is the simple one which points the plot by the "for`next" syntax and it writes an equation of the locus to output into it.
prog4 !The mobius change OPTION ARITHMETIC COMPLEX set window -3,3,-3,3 for t=0 to 2*pi step 0.01 ! The show of unit circle set line color 3 let z1=complex(cos(t),sin(t)) plot lines:re(z1),im(z1); next t set area color 3 paint 0,0 draw axes get point: p,q ! The setting central of circle let a=complex(p,q) for t=0 to 2*pi step 0.001 let z=complex(cos(t),sin(t))+a ! The circle which center is a let z2=conj(z) ! The conjugate complex let w=1/z ! reflection set line color 2 plot lines:re(z),im(z) ! The show of the locus set line color 7 plot lines:re(z2),im(z2) set line color 4 plot lines:re(w),im(w) next t END |
@When dispatching a program, it is expected that the near point to origin fades away from the origin and the point which left the origin approaches the origin. Because the point z on the circumference which is near the origin is moved to the infinite far point, the radius of the transformed circle approximates the infinity and the whole diagram approximates a straight line.
@Therefore, if assuming that the straight line is the circle in the wide sense, it finds that the moubius change is the change ( circle-to-circle correspondence ) which moves circle to circle.
@Moreover, the change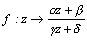 
is called complex linear change, this change is circle-to-circle correspondence from resolving 
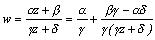. To assemble a program in Decimal BASIC and to confirm this will never be difficult.
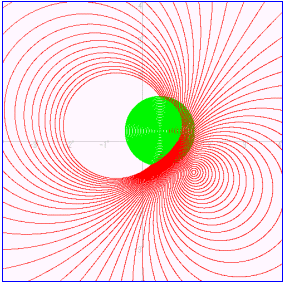@prog5> is the program to simulate what point the inside of the circle with radius 1 is moved to by the moubius change. In the program, the part of
@@@when exception in`use `end when
is the phrase of the exception condition. It will be impossible to carry out functions without this line. To have students discover and solve the errors/problems is what mathematics education should strive for.
@There is presentation software to show to the student plainly. However, there is little software with which a student himself can experiment and operate to examine the algorithm, estimate and confirm execution. The simplicity of use is one of Decimal BASIC's appealing qualities.
prog5
! The inner change of circle
set color mix(0) 0,0,0 ! The change of the background color
clear
option arithmetic complex
let s=4
set window -s,s,-s,s
draw axes
input prompt "a+bi=":a,b
set point style 1
for r=1 to 0 step -0.02
for t=0 to 2*pi step pi/3600
let z1=complex(a,b)
let z2=complex(r*cos(t),r*sin(t))
let z=z1+z2 ! The definition of circle
set point color 3
plot points:re(z),im(z) ! The show of circle
when exception in
let w=1/z
set point color 4
plot points:re(w),im(w) ! The show of mobius
use
end when
next t
next r
END
|