札幌新川高等学校 中村文則
十進BASICは、symple,speedy,sophisticatedなプログラム言語である｡
あまたの魅力ある機能はとても短い紙面で説明しきれるものではないが、ここでは、高校現場のサイドから、複素平面の指導における効果的利用に限定して、以下触れていく｡
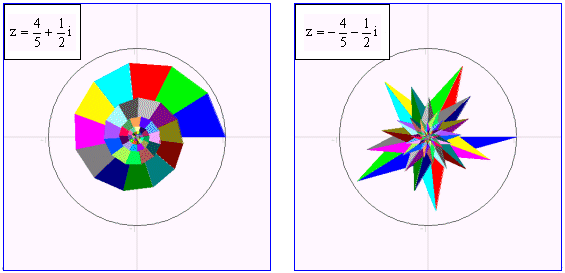
＜prog1＞は、複素数zのn乗を描画するプログラムである｡get point命令を使ってマウスにより複素数値を取得し、その累乗を色分けするが、マウスの位置により様々な、万華鏡のような色鮮やかな紋様が描かれる｡
十進BASICでは、ちょっとした画面効果の遊びを入れてもこんなに短いプログラムですんでしまうのである｡
＜prog1＞!複素数z^n表示 let s=1.5set window -s,s,-s,s draw axes option angle degrees for t=1 to 360 !単位円の描画 plot lines:cos(t),sin(t); next t get point:a,b !マウスによる複素数指定 print "z=";a;"+";b;"i" let c=angle(a,b) let r=sqr(a^2+b^2) for n=1 to 2000 !z^n の描画 set area color n+1 let n1=n-1 plot area:0,0; r^n*cos(n*c),r^n*sin(n*c); && r^n1*cos(n1*c),r^n1*sin(n1*c) next n end |
高校数学の現場では、複素平面の分野は厄介物として扱われる。行列の代替分野として登場したにも関わらず、変換としての指導はし難い｡行列が点の一次変換としてのoperatorであるに対して、複素平面では、複素数が複素数を変換するためである｡そのため、複素数問題は、z=x+yiと置き、水と油を分離するように、実部と虚部の値を求め、機械的に解く方法が横行してしまっている｡複素数が変換のイメージとして捉えにくいことが余計拍車をかけてしまう｡
しかし、十進BASICによる描画イメージの鮮やかさは、そんな不安を払拭する｡単に画像を見せることのインパクトのみならず、単純化されたプログラムを見せることで、より効果的なモチベーションを提示できる｡実際、prog1のように、座標設定、単位円の描画、数値の入力、偏角、絶対値の計算、描画というステップが実にシンプルに記録できる｡プログラムを読ませることで、複素数の変換の仕組みが一目瞭然、理解できてしまうのである｡
十進BASICには、「絵定義」という描画機能がある｡
図のデータを副プログラムとして記述しておくことにより、それを呼出し、平行移動、拡大縮小、回転、せん断といった変形をすることができる｡これらの変形は作用素として複素数がもつ変換そのものと考えることができる｡したがって、十進BASICは、点のみならず、集合の変換までも可能にしてしまうのである｡
＜prog2＞は、１辺の長さ１の正方形を大枠としてつくられた象(単位象)に複素数を乗じることでその変換後の像(象の像)を描画するプログラムである｡
＜prog2＞ !単位象のn乗変換 picture 象 !単位象の絵定義 set area color 色 plot area:0,0;0.25,0;0.25,0.2;0.6,0.2;0.6,0;0.85,0;0.85,0.5; & & 0.9,0.5; 0.9,0.1;1,0.1;1,0.9;0.9,1;0,1;-0.1,0.5;0,0.8;0,0 !象の体 plot lines:0.65,0.8;0.55,0.8;0.45,0.6;0.5,0.5;0.6,0.506 !象の耳 plot lines:0.85,0.7;0.82,0.64;0.79,0.66; !象の目 end picture set window -4,4,-4,4 option angle degrees draw grid let 色=2 draw 象 input prompt "a,b=":a,b let r1=sqr(a^2+b^2) !絶対値 let c1=angle(a,b) !偏角 if r1>1 then let s=0.02 else let s=-0.02 end if if c1<0 then let c1=360+c1 end if for r=1 to r1 step s !拡大・縮小表示 set draw mode hidden let 色=0 draw 象 with scale(r-s) draw grid let 色=5 draw 象 with scale(r) set draw mode explicit next r for c=0 to c1 step 1 !回転 set draw mode hidden let 色=0 draw 象 with scale(r)*rotate (c-1) draw grid let 色=7 draw 象 with scale(r)*rotate(c) set draw mode explicit next c LET 色=15 draw 象 end |
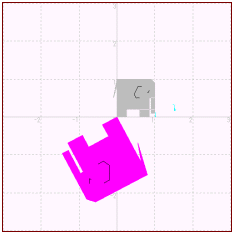複素数の大きさと偏角を計算し、for next命令を使い、伸縮、回転の順にアニメーションとして図形を変形し、動かしている｡図を動かす方法はいろいろあるが、ここでは、残像(象)を消すために、背景色でもう一度書き直すという手法をとっている｡
set draw mode hidden,explicitはそれぞれ、図をビットマップメモリで描く命令、それを画面に反映させる命令で、アニメーション時のちらつきを抑える十進BASIC独自の特殊処理である｡
ところで、このプログラムは10年ほど前、行列の一次変換の補助教材として、N88BASICで作成したものを移植したものである｡N88BASICのプログラムでは、line命令で結んだ線分ひとつひとつに一次変換の式を書き込み、気が付いたら膨大な行数のプログラムになってしまったものである｡絵定義による図形処理はそんな苦労を懐かしい思い出に変えてくれた｡
前述の２つのプログラムは、実際には複素数x+yiをデカルト座標上の点(x,y)に対応させ、その軌跡を描いているだけである｡したがって、プログラムは、複素数の性質を提示するわけではなく、性質の結果を表示しているに過ぎない｡
そしてそれが従来のBASICにおいては限界であったが、十進BASICには、数値を十進数として扱う以外に、複素数で表現するモードが用意されている。このモードにおいては、複素数の出力結果は、実部と虚部の対として括弧内に表される。また、
let i=sqr(-1) (あるいはlet i=complex(0,1) )
とすれば、虚数単位iを扱うことが可能になる｡
複素数モードの利用は高校数学Ｂにおける複素平面単元の指導の幅を大きく広げることになる｡
＜prog3＞は、入力した複素数の大きさ、偏角、そして２乗数を出力するものであるが、単に出力結果を見せるだけではなく、プログラムに触ることで問題を分析し、プログラムをいじることで統合的な知識の構築を図ることができる｡
例えば(prog1)については、複素数モードを設定して、for next 構文の描画のメイン部分を
plot area:0,0;re(z^n),im(z^n);re(z^n1),im(z^n1)
と書き換えることで、ガウス平面でn乗の描画が実行される｡両者のプログラムの違いと、出力結果の一致を比較すれば、ド-モアブルの定理等、複素数の性質が浮かび上がってくるのである｡
＜prog3＞ !複素数計算 OPTION ARITHMETIC COMPLEX OPTION ANGLE DEGREES input prompt "a,b=": a,b let z=complex(a,b) print "z=";re(z);"+";im(z);"i" print "|z|=";abs(z) print "arg(z)=:";arg(z) print "z^2=";re(z^2);"+";im(z^2);"i" END |
数学Bでの頻出問題を十進BASICで分析してみよう｡
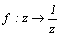なるfをメービウス変換というが、この変換の指導が、複素数変換の高校現場での難所となっている｡ 
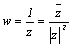から、wはzの共役複素数 
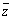を 
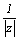倍に伸縮した数であることがわかる｡ 
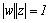となる関係は幾何でいう反転である｡したがってメービウス変換は、共役複素数の反転変換と考えることができる｡
複素平面上の単位円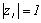 
に対して、中心αである半径1の円は、
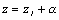と表現される｡この円周上の点zをメービウス変換した点 
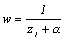の軌跡を求めてみよう。
＜prog4＞が軌跡の描画をするプログラムである｡for〜next構文で点をプロットしているだけの単純なものであり、出力したい軌跡の方程式をその中に書き込んでいる｡
プログラムを走らせると、原点により近い点は、原点から遠ざかり、原点からより離れた点は、原点に近づくことが予想される｡円周上の点zで原点に近い点は、無限遠点に移されるから、変換後の円の半径は無限大となり、図形全体は直線に近似する｡
＜prog4＞
!メービウス変換OPTION ARITHMETIC COMPLEX
set window -3,3,-3,3
for t=0 to 2*pi step 0.01 !単位円の描画
set line color 3
let z1=complex(cos(t),sin(t))
plot lines:re(z1),im(z1);
next t
set area color 3
paint 0,0
draw axes
get point: p,q !円の中心の設定
let a=complex(p,q)
for t=0 to 2*pi step 0.001
let z=complex(cos(t),sin(t))+a !中心aの円
let z2=conj(z) !共役複素数
let w=1/z !反転
set line color 2
plot lines:re(z),im(z) !軌跡の描画
set line color 7
plot lines:re(z2),im(z2)
set line color 4
plot lines:re(w),im(w)
next t
END
|
したがい、直線を広義の円とみなせば、メービウス変換は、円を円に移す(円々対応)変換であることが分かるのである｡
さらに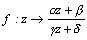 
なる変換を複素一次変換というが、
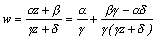と分解することで、この変換も円々対応である｡十進BASICでプログラムを組んでこのことを確認することは、けっして難しい作業ではないだろう｡
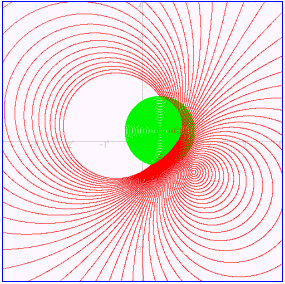＜prog5＞は、半径１の円の内部がメービウス変換で、どんな点に移されるかをシミュレートするものである｡プログラム中
when exception in〜use 〜end when
の部分は、例外状態の処理をする区である｡エラー発生時の緊急避難のことであるが、このことは、この構文がなければ実行上支障をきたすということである｡その原因を生徒に問いかけたり、例外処理を外したプログラムを提示しておいて、エラーが起きたり起きなかったりすることを生徒個々が発見し、バグを埋めていく思考過程は、ある意味では数学教育が希求するものであるといえるだろう｡
生徒に提示するだけのプレゼンテーションソフトはずいぶんある｡しかし、生徒自身が実際に、「触って、いじって」、アルゴリズムを調べ、実行を予測し、確認することができるソフトは少ない。電卓のような手軽さが、十進BASICの魅力のひとつであるといえる｡
＜prog5＞
!円の内部変換
set color mix(0) 0,0,0 !背景色の変更
clearoption arithmetic complex
let s=4
set window -s,s,-s,s
draw axes
input prompt "a+bi=":a,b
set point style 1
for r=1 to 0 step -0.02
for t=0 to 2*pi step pi/3600
let z1=complex(a,b)
let z2=complex(r*cos(t),r*sin(t))
let z=z1+z2 !円の定義
set point color 3
plot points:re(z),im(z) !円の描画
when exception in
let w=1/z
set point color 4
plot points:re(w),im(w) !メービウスの描画
use
end when
next t
next r
END
|