
乣偪傚偭偲曄偊偨n怓栤戣乣
嶥杫憯娾崅摍妛峑丂拞懞丂暥懃
仭仭仭丂偮偄偵乣S愭惗偑傗偭偰偟傑偭偨両丂仭仭仭
丂尒妛椃峴偺堷棪偱偳偭傉傝旀傟偰怑堳幒偵扝傝拝偔偲丆婘偺忋偵儗億乕僩偑抲偐傟偰偄偨丏怗傞偲傂傫傗傝偲偟偨姶怗丏偡偖偵S愭惗偺傕偺偲棟夝偟偨丏偄偮傕偺偙偲側偑傜S愭惗偺廃傝偵偼旝柇側僆乕儘儔偑偁傞丏嬌姦偺抧偱偟偐尒傜傟偸岝偺懷偱偁傞丏偦偺僆乕儘儔傪傑偲偭偨S愭惗偑抲偄偰偄偭偨傕偺偱偁傞丏
丂丂丂乽惓懡柺懱偺揾傝暘偗乿乣偪傚偭偲曄傢偭偨n怓栤戣乣丏
丂乽惓敧柺懱傪堎側傞俉怓偱揾傝暘偗傞曽朄偼壗捠傝偁傞偐乿丏夝摎偵峴偒媗偭偨枛偵悢妛弨旛幒偵懌傪塣傃丆俽愭惗偵彆尵傪偄偨偩偄偨栤戣偵娭偡傞儗億乕僩偱偁偭偨丏俽愭惗偼俆庬椶偺惓懡柺懱(僾儔僩儞偺懡柺懱)偺揾傝暘偗傪堦斒夝偲偟偰傑偲傔傜傟偨丏恄偺椞堟偵嬤偄僆僽僕僃偱偁傞惓懡柺懱側傜偽丆偦偺揾傝暘偗傕傗偼傝旤偟偔偁傜偹偽側傜側偄偲偺妋怣偺尦偵偦偺夝寛傪尒弌偟偰偄傞丏僉乕儚乕僪偼 丏柺傪慖傃怓傪弴師揾偭偰偄偔偺偱偼側偔丆怓傪揾傝廔偊偨(n!)屻偵丆捀揰偲幉偐傜懡柺懱偺僶儔儞僗傪峫椂偟偰偦偺攝怓偺廳側傝傪挷傋丆
丂丂丂(捀揰偺悢)亊(捀揰偺師悢)
側傞寢榑傪摼偰偄傞丏偙偙偱捀揰偺師悢偲偼侾捀揰偱愙偡傞曈偺悢偱偁傞丏
丂杮儗億乕僩偼丆俽愭惗偺寢榑偵暿偺懁柺偐傜敆傠偆偲偡傞傕偺偱偁傞丏偝傜偵偼丆侾俁庬椶偺弨惓懡柺懱丆偄傢備傞"傾儖僉儊僨僗偺棫懱"偵偮偄偰傕偦偺揾傝暘偗傪峫偊偰傒傞丏
(1) 侾柺傪愗傝敳偄偰揥奐偡傞(棫懱恾宍偐傜暯柺恾宍傊偺曄姺)
侾丏惓巐柺懱偺応崌
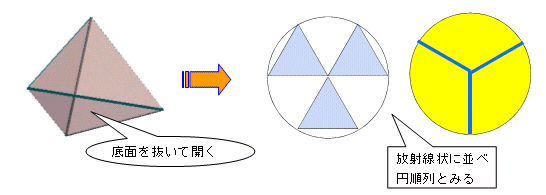
丂乽掙柺傪屌掕偡傞乿偲偼丆掙柺偵揔摉側怓傪巜掕偟偰乽揾偭偰偟傑偭偨乿偲傒偰丆巆傝偺俁柺傪揾傞偙偲偱偁傞丏偦偙偱丆偦偺掙柺傪愗傝敳偒丆巐柺懱傪曻幩慄忬偵揥奐偟偨恾宍偺揾傝曽傪峫偊傞偲傒側偡偙偲傕偱偒傞丏寢嬊偦傟偼丆墌廃傪俁摍暘偟偰暘偗傜傟傞晹暘偺墌弴楍偺怓暘偗偵堦抳偡傞丏傛偭偰
丂丂丂(3-1)!=2丂捠傝
偲側傞丏
俀丏惓榋柺懱偺応崌
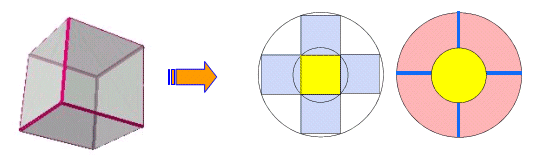
丂惓巐柺懱偲摨條偵丆掙柺偺惓曽宍傪敳偄偰揥奐偡傞偲丆壓恾偺傛偆側墌廃傪係摍暘偟偨恾宍偺揾傝暘偗傪峫偊傟偽傛偄丏偟偨偑偭偰丆拞墰偺墌丆係偮偺愵宍偺弴偵揾偭偰偄偔偲丆
丂丂丂5C1亊(4-1)!=30丂捠傝
偲側傞丏
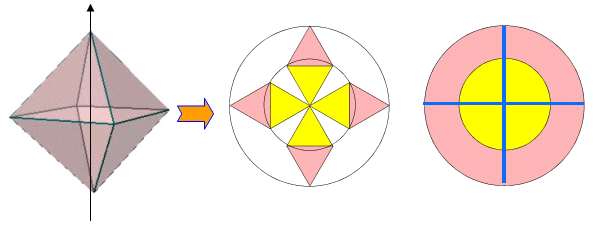
俁丏惓敧柺懱偺応崌
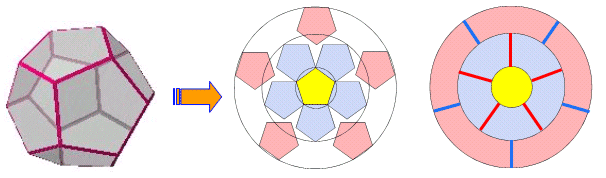
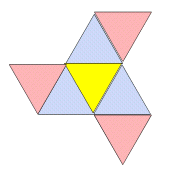 丂摨條偵掙柺傪敳偔偲丆偙偺応崌偼塃恾偺傛偆側晽幵偺宍偵揥奐偝傟傞丏偙偺恾偱偼丆拞墰偺嶰妏宍偺奜懁偵俇偮偺嶰妏宍偑攝楍偝傟偰偄傞傛偆偵尒偊傞偑丆偙傟偑岆偭偨夝朄偺梫場偲側傞丏拞墰偺嶰妏宍偵懕偒丆奜懁偺俇偮偺嶰妏宍傪揾偭偰偄偔偲丆
丂摨條偵掙柺傪敳偔偲丆偙偺応崌偼塃恾偺傛偆側晽幵偺宍偵揥奐偝傟傞丏偙偺恾偱偼丆拞墰偺嶰妏宍偺奜懁偵俇偮偺嶰妏宍偑攝楍偝傟偰偄傞傛偆偵尒偊傞偑丆偙傟偑岆偭偨夝朄偺梫場偲側傞丏拞墰偺嶰妏宍偵懕偒丆奜懁偺俇偮偺嶰妏宍傪揾偭偰偄偔偲丆
丂丂丂7C1亊(6-1)!=840丂捠傝
偲側傞偑丆嶰妏宍偺岦偒傪峫椂偡傞偲丆拞墰偺嶰妏宍偲曈傪嫟桳偟偰偄傞俁偮偺嶰妏宍偼丆侾捀揰傪嫟桳偡傞巆傝偺俁偮偺嶰妏宍偲偼摨攝楍偵偡傞偙偲偼偱偒側偄偙偲偑傢偐傞丏偦偙偱丆乽揥奐偡傞乿偲偄偆偙偲傪傕偭偲廮擃偵夝庍偟偰傒傛偆丏
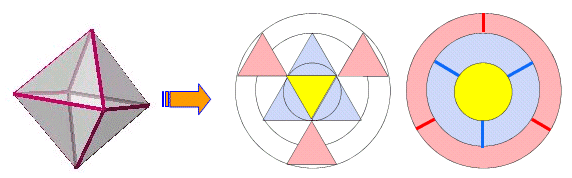
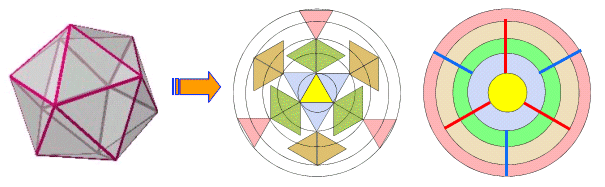
丂乽愗傝棧偟偰攝楍偡傞乿偙偲傕揥奐偡傞偲傒側偟丆壓恾偺傛偆偵曻幩慄忬偵攝楍偡傞丏摨怱墌偑俁偮偱偒傞偑丆撪懁偺墌偐傜揾偭偰偄偙偆丏偙偙偱俀斣栚偺墌偼墌弴楍偩偑丆屌掕偟偰怓傪揾傞偙偲偱堦斣奜懁偺墌偼丆偨偩偺弴楍偲側傞偙偲偵拲堄偡傞丏偟偨偑偭偰丆
丂丂丂7C1亊6C3亊2亊3!=1680丂捠傝
係丏惓侾俀柺懱丒惓20柺懱偺応崌
丂偦傟偧傟揾傝暘偗曽偼丆
丂丂丂惓12柺懱丂仺丂11C1亊10C5亊4!亊5!
丂丂丂惓20柺懱丂仺丂19C1亊18C3亊2!亊15P6亊9P6亊3!
偲側傞丏
俆丏惓n柺懱偺揾傝暘偗偺堦斒壔
丂惓20柺懱偺揥奐恾傪尒傞偲丆撪懁偐傜俁偮丆係偮傔偵攝楍偝傟偰偄傞惓嶰妏宍偺岦偒偼偦傟偧傟俀庬椶偁傞偐傜丆偙傟偼摨攝楍偱偒側偄偙偲偵側傞偑丆慜暸偱偼偦傟傪柍帇偟偨寁嶼傪偟偰偄傞丏偙傟偼丆撪懁偐傜俀斣栚偺墌偺攝楍偼丆侾偮偺嶰妏宍傪屌掕偡傞偙偲偱丆椺偊傟偽夢偭偰偄傞撈妝偺摦偒傪巭傔偰偟傑偭偨傢偗偱丆偦傟埲奜偺摨怱墌偺攝楍偼偨偩偺弴楍偲傒側偡偙偲偑壜擻偲側傞丏偟偨偑偭偰丆惓20柺懱偺揾傝暘偗偼丆
丂丂丂19C1亊18C3亊2!亊15!
偲偟偰傕傛偄偙偲偵側傞丏偝傜偵丆嵟弶偵撪懁偐傜俀斣栚偺摨怱墌傪揾偭偰偟傑偆偲丆
丂丂丂19C3亊2!亊16!
偲娙扨偵傑偲傔傜傟傞丏偙傟偐傜丆惓n柺懱偺揾傝暘偗傪媮傔偰傒傛偆丏
丂惓n柺懱偺侾偮偺柺偑惓m妏宍偱偁傞偲偡傞丏偙偺惓m妏宍偺傂偲偮傪愗傝敳偄偰丆偦偙偐傜曻幩忬偵揥奐偟偰偄偔偲丆摨怱墌偺拞怱偵侾偮偺惓m妏宍偑抲偐傟傞丏偦偟偰惓m妏宍偺曈偺悢m偩偗丆偦偺廃傝偵惓m妏宍偑墌弴楍偲偟偰攝楍偝傟傞偙偲偐傜丆
丂丂丂n-1Cm亊(m-1)!(n-m-1)!丂捠傝
偙傟偑揾傝暘偗偺憤悢偲側傞丏
(2) 捀揰偺廃傝偵曻幩慄忬偵揥奐偡傞(惓懡柺懱傪撈妝偲傒傞)
丂惓懡柺懱偼偳偺捀揰偵懳偟偰傕捀揰傪幉偲偡傞懳徧側恾宍偲側傝丆幉傪夞揮偺拞怱偲偟偰撈妝偺傛偆偵夢偡偙偲偑壜擻偲側傞丏偙偺偙偲傪棙梡偟偰丆惓懡柺懱偺揾傝暘偗傪峫偊偰傒傛偆丏
侾丏惓榋柺懱偺応崌
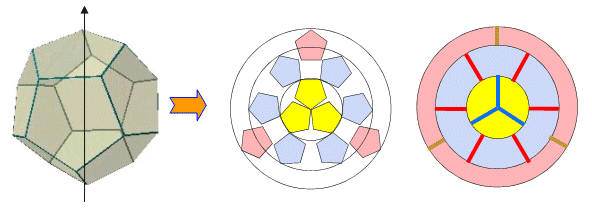
丂惓榋柺懱偺侾捀揰傪抧柺偵偍偄偰撈妝偺傛偆偵棫偰丆捀揰偐傜曻幩慄忬偵愗傝奐偔偲壓恾偺傛偆偵攝抲偝傟傞丏偟偨偑偭偰偦偺揾傝暘偗曽偼丆6C3亊2!亊3!捠傝偲側傞偑丆惓俇柺懱偺俉偮偺捀揰偄偢傟偵偍偄偰傕摨條偺揾傝暘偗曽偑峫偊傜傟傞偙偲傛傝丆偦偺憤悢偼丆
丂丂丂6C3亊2!亊3!亊1/8=30丂捠傝
偲側傞丏
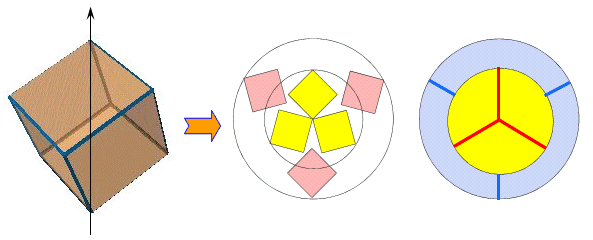
俀.惓係柺懱偺応崌
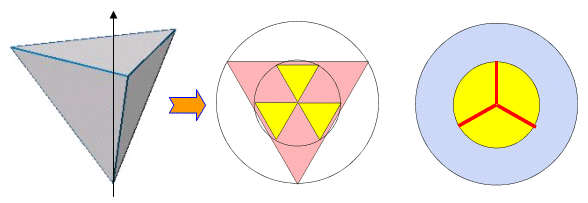
丂惓係柺懱傪丆捀揰傪幉偲偟偰抧柺偵棫偰傞偲丆抧柺偵暯峴側忋柺偑偱偒傞偐傜丆曻幩慄忬偵偼揥奐偱偒側偄丏偦偙偱丆捀揰傪揰岝尮偲偟偨偲偒偺塭傪揥奐恾偲傒側偡偲壓恾偺傛偆偵側傞丏偟偨偑偭偰偦偺揾傝暘偗曽偼丆
丂丂丂4C3亊2!亊1亊1/4=2丂捠傝
俁.惓俉柺懱丒惓侾俀柺懱丒惓俀侽柺懱偺応崌
丂巆傝偺懡柺懱偵偮偄偰傕摨條偵揥奐偟偨傕偺偑壓恾偱偁傞丏
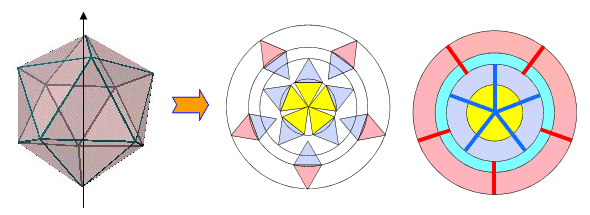
係丏惓n柺懱偺揾傝暘偗偺堦斒壔
丂捀揰偺廃傝偺(捀揰傪嫟桳偡傞)柺偺屄悢傪r(捀揰偺師悢)丆捀揰偺屄悢傪s偲偡傞丏捀揰傪幉偲偟偰懡柺懱偑夞揮偡傞偲偒丆捀揰偺廃傝偺柺偺揾傝暘偗偼丆nCr亊(r-1)!丏偙偺揾傝暘偗偱懡柺懱僐儅偼掆巭偡傞偐傜偦傟埲奜偺柺偺怓偺揾傝曽偼丆(n-r)!偲側傞丏捀揰偺屄悢偩偗摨偠揾傝曽偑峫偊傜傟傞偐傜丆埲忋傛傝丆揾傝暘偗偺憤悢P(n)偼
丂丂丂P(n)=nCr亊(r-1)!亊(n-r)!亊1/s丂捠傝
偱偁傞丏
丂師偵丆偙偺幃傪彮偟惍棟偟偰傒傛偆丏
丂丂丂P(n)=nCr亊r!/r亊(n-r)!亊1/s=n!/rs
俽愭惗偵傛偭偰帵偝傟偨寢榑偑摼傜傟偨丏
偲偙傠偱丆偙偺幃偱暘曣偼
丂丂(捀揰偺屄悢)亊(捀揰偺廃傝偺柺偺屄悢)丂丂丂乧乧(*)
傪昞偡偑丆師偺傛偆偵峫偊傞偙偲傕偱偒傞丏
丂惓n妏宍偺捀揰偺屄悢s偼丆柺偑惓m妏宍偱偁傞偲偒丆捀揰悢偼mn屄偱偒傞偑丆侾捀揰偺廃傝偺柺r偺悢偩偗廳側傞偐傜丆
丂丂丂s=mn亊1/r
側傞娭學偑惉傝棫偮丏偙傟偐傜
丂丂丂rs=mn
偡側傢偪丆(*)偼丆
丂丂丂(惓懡妏宍偺曈偺屄悢)亊(惓懡柺懱偺柺偺屄悢)
偵摍偟偄丏傛偭偰
丂丂丂P(n)=n!/rs=n!/mn=(n-1)!/m
偲側傞丏埲忋傛傝丆
丂惓懡柺懱偺揾傝暘偗曽偺憤悢偼丆惓n柺懱偑惓m妏宍偱峔惉偝傟傞偲偒丆丂丂
丂丂丂丂(n-1)!/m丂捠傝
偱偁傞丏
|
壓昞偑惓懡柺懱偺揾傝暘偗悢偱偁傞丏
| 惓懡柺懱 |
惓係柺懱 |
惓俇柺懱 |
惓俉柺懱 |
惓12柺懱 |
惓俀侽柺懱 |
| 惓懡妏宍 |
惓嶰妏宍 |
惓曽宍 |
惓嶰妏宍 |
惓屲妏宍 |
惓嶰妏宍 |
| 揾傝暘偗悢 |
3!/3
=2 |
5!/4
=30 |
7!/3
=1680 |
11!/5
=7983360 |
19!/3
=40548366802944000 |
俆丏曗懌
丂侾柺傪愗傝敳偄偰揥奐偡傞偙偲傛傝摼傜傟偨幃傪曄宍偡傞偲丆
丂丂丂n-1Cm亊(m-1)!(n-m-1)!=(n-1)!/(n-m-1)m!亊(m-1)!(n-m-1)!=(n-1)!/m
丂丂丂丂
(俁) 弨惓懡柺懱偺揾傝暘偗曽
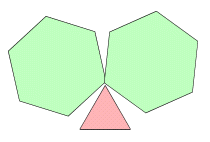 丂惓懡柺懱偺僇僪(捀揰)傪偦偓棊偲偡偲怴偨側棫懱偑弌尰偡傞丏椺偊偽惓巐柺懱偺係偮偺捀揰傪曈偺嶰摍暘揰偱愗傝棊偲偡偲丆惓嶰妏宍偺愗傝岥偑係偮偱偒丆惓巐柺懱偺柺偺悢(係)偩偗惓榋妏宍偑嶌傜傟傞丏偲偙傠偱丆偙偺棫懱偺奺捀揰偺廃傝偺懡妏宍偺攝楍傪傒傞偲丆傒側摍偟偔塃恾偺傛偆偵攝抲偝傟偰偄傞偙偲偑暘偐傞丏
丂惓懡柺懱偺僇僪(捀揰)傪偦偓棊偲偡偲怴偨側棫懱偑弌尰偡傞丏椺偊偽惓巐柺懱偺係偮偺捀揰傪曈偺嶰摍暘揰偱愗傝棊偲偡偲丆惓嶰妏宍偺愗傝岥偑係偮偱偒丆惓巐柺懱偺柺偺悢(係)偩偗惓榋妏宍偑嶌傜傟傞丏偲偙傠偱丆偙偺棫懱偺奺捀揰偺廃傝偺懡妏宍偺攝楍傪傒傞偲丆傒側摍偟偔塃恾偺傛偆偵攝抲偝傟偰偄傞偙偲偑暘偐傞丏
丂偙偺傛偆偵丆棫懱偺奺捀揰偺廃傝偺恾宍偺攝抲偑傒側摍偟偄恾宍傪弨惓懡柺懱偲偄偄丆惓巐柺懱偐傜嶌傜傟傞棫懱傪愗摢巐柺懱偲偄偆丏傾儖僉儊僨僗偼偙偺旤偟偄棫懱偵嫽枴傪傕偪丆尋媶傪廳偹丆侾俁屄偺弨惓懡柺懱傪敪尒偟偨丏偦偺弨惓懡柺懱傪傾儖僉儊僨僗偺懡柺懱偲傕偄偆丏偝傜偵丆偦偺屻偺尋媶偱尰嵼偼侾俇屄偁傞偙偲偑抦傜傟偰偄傞丏偙偙偱偼傾儖僉儊僨僗偺懡柺懱偵尷掕偟偰偦偺揾傝暘偗曽傪挷傋偰傒傛偆丏
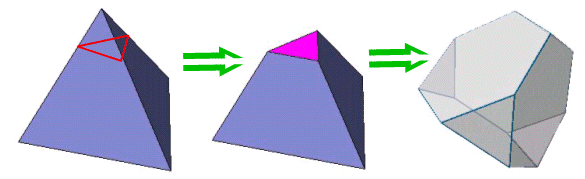
侾丏愗摢巐柺懱
 丂掙柺傪屌掕偟偰揾偭偰傒傛偆丏柺悢偼丆傕偲偺惓懡柺懱偺捀揰悢+柺悢偱偁傞偐傜俉怓偱揾傝暘偗傞偙偲偵側傞丏掙柺傪惓嶰妏宍偲偡傞偲丆俁偮偺惓屲妏宍偑曈傪嫟桳偡傞偙偲丆媦傃惓嶰妏宍偺屄悢偑俆屄偱偁傞偙偲偐傜丆偦偺揾傝暘偗曽偼丆
丂掙柺傪屌掕偟偰揾偭偰傒傛偆丏柺悢偼丆傕偲偺惓懡柺懱偺捀揰悢+柺悢偱偁傞偐傜俉怓偱揾傝暘偗傞偙偲偵側傞丏掙柺傪惓嶰妏宍偲偡傞偲丆俁偮偺惓屲妏宍偑曈傪嫟桳偡傞偙偲丆媦傃惓嶰妏宍偺屄悢偑俆屄偱偁傞偙偲偐傜丆偦偺揾傝暘偗曽偼丆
丂丂丂8C3亊2!亊5!亊1/4=3360丂捠傝
偲側傞丏傑偨丆掙柺傪惓屲妏宍偵偟偨応崌傕摨條偺寁嶼幃偑摼傜傟傞丏
丂偱偼丆捀揰傪幉偲傒偰丆偦偺攝楍傪峫偊傞偲偳偆側傞偱偁傠偆偐丏捀揰偺廃傝偺恾宍偺攝抲傪傒傞偲墌弴楍偲偼側傜側偄偐傜丆柺悢偺揾傝曽傪扨弮偵捀揰悢偱妱偭偨傕偺偑偦偺抣偲側傞丏捀揰悢偼惓巐柺懱偺捀揰悢係傛傝丆係亊俁亖侾俀偱偁傞偐傜丆
丂丂丂8!/12=3360丂捠傝
偲側傞丏
俀丏棫曽敧柺懱
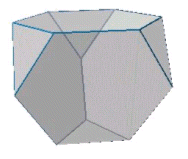
 丂棫曽懱偺僇僪傪曈偺拞揰偱愗傝庢傞偲弌棃忋偑傞丏偁傞偄偼丆惓敧柺懱偺曈偺拞揰傪愗偭偰僇僪傪偲偭偰傕偱偒傞偐傜丆偙偺柤傪姤偡傞丏塃恾偐傜暘傞傛偆偵丆惓嶰妏宍俉屄偲惓曽宍俇屄偐傜峔惉偝傟傞丏柺傪屌掕偟偰揾傝暘偗傪峫偊傞偲丆偦偺柺偺宍偵傛傝師偺俀捠傝偺寁嶼偑峫偊傜傟傞丏
丂棫曽懱偺僇僪傪曈偺拞揰偱愗傝庢傞偲弌棃忋偑傞丏偁傞偄偼丆惓敧柺懱偺曈偺拞揰傪愗偭偰僇僪傪偲偭偰傕偱偒傞偐傜丆偙偺柤傪姤偡傞丏塃恾偐傜暘傞傛偆偵丆惓嶰妏宍俉屄偲惓曽宍俇屄偐傜峔惉偝傟傞丏柺傪屌掕偟偰揾傝暘偗傪峫偊傞偲丆偦偺柺偺宍偵傛傝師偺俀捠傝偺寁嶼偑峫偊傜傟傞丏
丂柺偑惓嶰妏宍丂14C3亊2!亊11!亊1/8
丂柺偑惓曽宍丂丂14C4亊3!亊10!亊1/6
丂師偵丆捀揰偺廃傝偺攝楍傪傒傞偲丆塃恾偺傛偆偵側傞丏傑偨丆捀揰悢偼丆捀揰偺廃傝偺恾宍偺屄悢偐傜丆
丂丂丂(3亊8+4亊6)/4=12
傛偭偰丆揾傝暘偗偺憤悢偼丆
丂丂丂14C2亊12!亊1/12丂捠傝
偲側傞丏
俁丏傾儖僉儊僨僗偺懡柺懱偺怓偺揾傝暘偗
丂弨惓懡柺懱偺揾傝暘偗傪堦斒壔偟傛偆丏
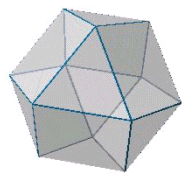
丂傑偢丆柺丆捀揰偺偄偢傟偐偱峫偊傞偐偱偁傞偑丆柺偱偼柺偺廃傝偺恾宍偺攝抲偑暋嶨側懡柺懱傕偱偰偔傞丏椺偊偽塃恾偼丆惓嶰妏宍偲惓屲妏宍偱峔惉偝傟傞弨惓懡柺懱偱丆偹偠傟廫擇柺懱偲偄偆丏傾儖僉儊僨僗偺棫懱偱偼傕偭偲傕懡偄柺傪傕偮棫懱偱偁傝丆92柺懱偲側傞丏偙偺恾宍偱偼嶰妏宍偺廃傝偺攝抲傪峫偊傞偲丆俀僷僞乕儞偁傞偨傔丆廳暋偡傞応崌偺悢傪媮傔傞偙偲偑擄偟偔側傞丏偱偼丆捀揰傪幉偲傒偰寁嶼偡傞偲偳偆側傞偩傠偆偐丏弨惓懡柺懱偺掕媊傛傝丆捀揰偺廃傝偺恾宍偺攝抲偼傒側摍偟偔丆恾偺傛偆偵丆係偮偺惓嶰妏宍偲丆侾偮偺惓屲妏宍偱偁傞丏偙偺攝抲偼墌弴楍偱偼側偄偐傜丆偦偺揾傝暘偗曽朄偼92!傪捀揰悢偱妱偭偰摼傜傟傞丏偝偰丆栤戣偼偦偺捀揰悢偱偁傞偑丆惓嶰妏宍偺屄悢80丆惓屲妏宍偺屄悢12偐傜丆
丂丂丂(80亊3+12亊5)/5=80丂捠傝
偲媮傔傜傟傞丏埲忋傛傝丆
丂丂丂92!/80丂捠傝
偲偄偆揤暥妛揑側抣傪摼傞丏
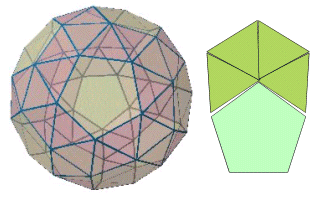
丂偙偺傛偆偵丆揾傝暘偗偼捀揰偺廃傝偺恾宍偺攝抲偲捀揰悢偵傛傝丆寁嶼偝傟傞偑丆傾儖僉儊僨僗偺懡柺懱偺応崌丆攝抲偑墌弴楍偵側傞傕偺偼幚偼俀庬椶偟偐側偄丏傂偲偮偼愭偵嫇偘偨棫曽敧柺懱偱偁傝丆傕偆傂偲偮偼丆惓嶰妏宍偲惓屲妏宍偱峔惉偝傟傞廫擇丒擇廫柺懱偱偁傞丏偙偺棫懱偼丆惓12柺懱傑偨偼惓20柺懱偺奺曈偺拞揰偐傜僇僪傪愗傝棊偲偟偰偄偔偲嶌傜傟丆捀揰偺廃傝偼棫曽敧柺懱偲摨偠攝楍偵側偭偰偄傞丏
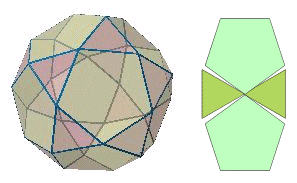
傛偭偰丆傾儖僉儊僨僗偺懡柺懱偺揾傝暘偗憤悢偼丆師幃偱摼傜傟傞丏
柺悢n丆捀揰悢s偱偁傞偲偒丆堎側傞怓偱揾傝暘偗傞応崌偺悢偼
丂丂丂棫曽敧柺懱偲廫擇丒擇廫柺懱丂丂丂乧乧丂nC2亊(n-2)!亊1/s=n!/2s丂捠傝
丂丂丂偦傟埲奜偺傾儖僉儊僨僗偺懡柺懱丂乧乧丂n!/s 捠傝
|
係丏捀揰偺屄悢丂(僨僇儖僩偺掕棟)
丂捀揰悢偼丆捀揰偺廃傝偺恾宍偺攝抲偐傜摼傜傟傞偑丆捀揰偺愲搙偐傜媮傔傞偙偲傕壜擻偱偁傞丏偙偙偱丆愲搙偲偼丆捀揰傪嫟桳偡傞恾宍偺捀妏偺榓傪360亱偐傜堷偄偨抣偱偁傞丏偙傟偼暯柺恾宍偵偍偄偰偼奜妏偵憡摉偡傞傕偺偱偁傞丏
丂椺偊偽丆惓巐柺懱偼侾捀揰傪俁偮偺惓嶰妏宍偑嫟桳偟丆偦偺妏搙偺榓偼180亱偱偁傞偐傜丆愲搙偼丆 偱偁傞丏傑偨丆惓敧柺懱偼丆侾捀揰傪俁偮偺惓曽宍偑嫟桳偟丆妏搙偺榓偑270亱傛傝丆愲搙偼 偱偁傞丏愲搙偵偼師偵娭學偑偁傞偙偲偑抦傜傟偰偄傞丏

傛偭偰丆傾儖僉儊僨僗偺懡柺懱偺揾傝暘偗憤悢偼丆師幃偱摼傜傟傞丏
丂偙傟傪僨僇儖僩偺掕棟偲偄偆丏
丂幚嵺丆惓係柺懱丆惓俇柺懱偺捀揰悢偼偦傟偧傟丆係屄丆俉屄偱偁傞偐傜梕堈偵妋擣偱偒傞丏
丂偝偰丆偙偺偙偲偐傜丆媡偵弨惓懡柺懱偺捀揰悢偼丆捀揰偺廃傝偺恾宍偺妏搙偺崌寁偐傜傕媮傔傞偙偲偑偱偒傞偙偲偵側傞丏
丂丂丂捀揰悢=720亱/愲搙
偱偁傞丏椺偊偽丆惓敧柺懱偼丆捀揰偵係偮偺惓嶰妏宍偑偁傞偐傜丆愲搙=360亱-4亊60亱=120亱
傛偭偰丆
丂丂丂捀揰悢=720亱/120亱=6
偲側傞丏
俆丏捀揰偐傜懡柺懱偺忣曬傪廤傔傞
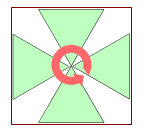 丂惓懡柺懱丒弨惓懡柺懱偼偲傕偵丆乽偡傋偰偺捀揰偺廃傝偺攝楍偑摍偟偄乿懡柺懱偱偁傞偐傜丆偦偺攝楍傪傒傞偙偲偱丆傕偲偺懡柺懱傪梊憐偡傞偙偲偑偱偒傞丏
丂惓懡柺懱丒弨惓懡柺懱偼偲傕偵丆乽偡傋偰偺捀揰偺廃傝偺攝楍偑摍偟偄乿懡柺懱偱偁傞偐傜丆偦偺攝楍傪傒傞偙偲偱丆傕偲偺懡柺懱傪梊憐偡傞偙偲偑偱偒傞丏
丂塃恾偱偼捀揰偺廃傝偵係偮偺惓嶰妏宍偑攝抲偝傟偰偄傞丏偟偨偑偭偰丆傕偲偺恾宍偼惓懡柺懱偱偁傞丏捀揰偺愲搙偼丆360亱-4亊60亱=120亱傛傝丆捀揰偺屄悢V偼
丂丂丂V=720亱/120亱=6
偱偁傞丏傑偨丆捀揰傪嫟桳偡傞曈偺杮悢偼係杮傛傝丆俇偮偺捀揰偱偼24杮偺曈偑偁傞偑丆偳偺曈傕2曈傪嫟桳偡傞偐傜丆曈偺杮悢E偼丆
丂丂丂E=24/2=12
偱偁傞丏嵟屻偵柺偺屄悢F偱偁傞偑丆係偮偺嶰妏宍偑捀揰傪嫟桳偡傞偙偲偐傜丆
丂丂丂V=3亊f/4
偑側傝偨偮丏偙傟偐傜丆
丂丂丂F=4亊6/3=8
傛偭偰丆傕偲偺懡柺懱偼惓敧柺懱偱偁傞偙偲偑傢偐傞丏
丂偱偼丆塃恾偺応崌偼偳偆偩傠偆偐丏
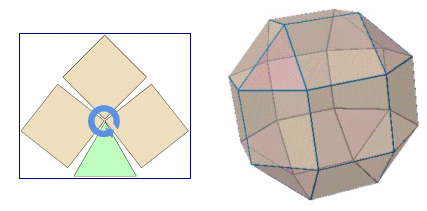
愲搙偼30亱偱偁傞偐傜捀揰悢偼
丂丂丂V=720亱/30亱=24
捀揰傪嫟桳偡傞曈偺杮悢偼係杮傛傝丆
丂丂丂E=4亊24/2=48
丂惓嶰妏宍偺屄悢傪F3丆惓曽宍偺屄悢傪F4偲偡傞偲丆係偮偺懡妏宍偑捀揰傪嫟桳偡傞偙偲傛傝丆
丂丂丂V=(3亊F3+4亊F4)/4
傛傝丆3F3+4F4=96丂乧乧嘆
丂傑偨丆捀揰偵廤傑傞嶰妏宍偲巐妏宍偺曈偺斾偼侾丗俁偱偁傞偙偲傛傝丆懡柺懱慡懱偺曈偺杮悢偺斾傕摨偠偱偁傞偐傜
丂丂丂F=F3+F4=26丂乧乧嘇丂
丂嘆丆嘇傛傝丆F3=8丆F4=18偱偁傞丏傛偭偰丆
丂丂丂F=F3+F4=26
丂偙偺懡柺懱偼丆柺俁屄偺惓嶰妏宍偲丆侾俉屄偺惓曽宍偱嶌傜傟偰偍傝丆旽宍棫曽俉柺懱(幬棫曽俉柺懱)偲偄傢傟偰偄傞傕偺偱偁傞丏
丂偱偼嵟屻偵塃恾偺懡柺懱丏
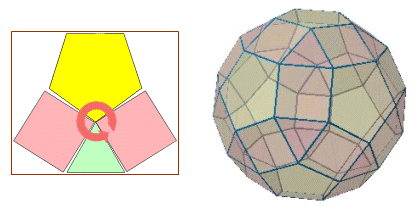
丂惓嶰妏宍丆惓曽宍丆惓屲妏宍偺俁庬椶偺惓懡妏宍偑捀揰偵廤傑偭偰偄傞丏
捀揰偺廃傝偺妏搙偺榓偼丆
丂丂丂60亱+2亊90亱+(180亱-360亱/5)=348亱
傛偭偰丆愲搙偼12亱偱偁傞偐傜丆
丂丂丂V=720亱/12亱=60
師偵丆曈偺杮悢偼丆
丂丂丂E=60亊4/2=120
惓嶰妏宍丆惓曽宍丆惓屲妏宍偺柺悢傪F3丆F4丆F5偲偡傞偲丆
丂丂丂3F3+4F4+5F5=4亊60丂乧乧嘆
傑偨丆 3F3:4F4:5F5=1:2:1
偦偙偱丆3F3=k丆4F4=30丆5F5=k偲偍偔偲丆嘆傛傝k=60
丂傛偭偰丆 F3=20丆F4=30丆F5=12
傪摼傞丏埲忋傛傝丆
丂丂丂F=F3+F4+F5=60
偲側傞丏偙偺暋嶨側懡柺懱傪旽宍廫擇丒擇廫柺懱偲偄傢傟傞傕偺偱偁傞丏
丂偲偙傠偱忋偺幃偺寁嶼壖掕偐傜斾椺掕悢k偺抣偑捀揰悢V偵摍偟偄偙偲傪撉傒庢傞偺偼梕堈偱偁傠偆丏埲忋傛傝丆師偺寢榑傪摼傞丏
丂弨惓懡柺懱偺捀揰丆曈丆柺偺屄悢傪偦傟偧傟丆V,E,F偲偡傞丏
丂惓k妏宍偺屄悢傪Fk屄丆捀揰偺廃傝偺屄悢傪nk屄偲偡傞偲偒丆
丂丂丂V=720亱/愲搙丆丂丂丂丂E=V儼nk/2
丂丂丂Fk=nkV/k丆丂丂F=儼Kk
|
丂偙偺傛偆偵丆僆僀儔乕偺掕棟偵埶傜側偔偰傕丆捀揰偺廃傝偺惓懡妏宍偺攝抲傪傒傞偙偲偱丆弨惓懡柺懱偼丆柺丆曈丆捀揰傪媮傔傞偙偲偑壜擻側偺偱偁傞(僨僇儖僩偺掕棟偺徹柧偵偼僆僀儔乕偺掕棟傪巊偆偐傜丆娫愙揑偵偼娭梌偟偰偄傞偺偩偑)丏
丂偙偺偙偲偐傜丆懡柺懱偺怓暘偗偵傕偟偨偑偭偰偡傋偰偺忣曬偺廤愊揰偱偁傞捀揰偐傜峫嶡偡傞偺偑嬌傔偰帺慠偱偁傞偲偄偊傞偺偱偁傞丏
俇丏僒僢僇乕儃乕儖偺揾傝暘偗偺憤悢傪媮傔傛偆
丂惓擇廫柺懱偺僇僪傪曈傪嶰摍暘偡傞揰偱愗傝棊偲偟偰偱偒傞懡柺懱偼丆傾儖僉儊僨僗偺懡柺懱偺拞偱傕偭偲傕桳柤側傕偺偱偁傞丏偁偺僒僢僇乕儃乕儖偱偁傞丏
丂偱偼丆嵟屻偵偙偺僒僢僇乕儃乕儖偺揾傝暘偗傪偟偰傒傛偆丏
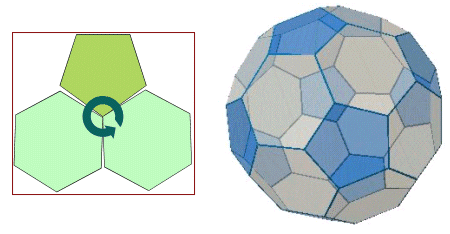
丂傑偢丆侾捀揰偐傜摼傜傟傞忣曬傪撉傒庢偭偰偄偔丏
丂捀揰偺廃傝偺妏搙偺榓偼丆
丂丂丂(180亱-360亱/5)+2亊(180亱-360亱/6)=348亱
傛傝丆愲搙偼丆
丂丂丂360亱-348亱=12亱
丂傛偭偰丆捀揰偺屄悢偼丆
丂丂丂V=720亱/12亱=60
丂師偵曈偺杮悢偼丆
丂丂丂E=60亊3/2=90
丂惓屲妏宍丆惓榋妏宍偺屄悢傪F5,F6偲偡傞偲丆捀揰偺廃傝偺屄悢偼偦傟偧傟侾屄丆俀屄偱偁傞偐傜丆
丂丂丂F5=60亊1/5=12
丂丂丂F6=60亊2/6=20
偟偨偑偭偰丆柺悢偼丆
丂丂丂F=F5+F6=32
偲側傞丏
丂埲忋傛傝丆僒僢僇乕儃乕儖偼丆惓屲妏宍偑12丆惓榋妏宍偑20偺暪偣偰32柺偱嶌傜傟丆捀揰偺廃傝偵偼丆惓屲妏宍侾偮偲惓榋妏宍俀偮偑攝抲偝傟傞丏傑偨丆偙偺俀偮偺惓懡妏宍偺攝抲偼墌弴楍偵偼側傜側偄偐傜丆偦偺怓偺揾傝暘偗偼丆
丂丂丂21!/60=4385513948894892169453633536000000丂捠傝
偲側傞丏
(Notes)乽愲搙偺榓偑 偱偁傞乿偙偲偺徹柧
丂懡柺懱傪峔惉偡傞傂偲偮偺柺偑m妏宍偱偁傞偲偡傞偲丆(m-2)杮偺懳妏慄傪堷偔偙偲偵傛傝丆m妏宍偼(m-1)屄偺嶰妏宍偵暘妱偝傟傞丏偟偨偑偭偰丆偡傋偰偺懡柺懱偺柺偼嶰妏宍偲傒側偟偰傕傛偄偙偲偵側傞丏
丂偙偙偱丆嶰妏宍偵暘偗偨応崌偺柺悢丆曈悢丆捀揰悢傪偦傟偧傟丆F,E,V偲偡傞偲丆偙偺懡柺懱偵偍偄偰傕丆僆僀儔乕偺掕棟
丂丂丂V+F-E=2
偼惉棫偡傞丏
丂柺悢偲曈悢偺娭學傪挷傋偰傒傛偆丏柺偼偡傋偰嶰妏宍偩偐傜丆傂偲偮偺柺偺曈偺杮悢偼俁杮丆嶰妏宍偼柺悢偩偗偁傞偐傜偦偺憤悢偼 丏柺偲柺偼侾曈傪嫟桳偡傞偙偲傪峫偊傞偲丆
丂丂丂E=3F/2
側傞娭學偑惉棫偡傞丏
丂傑偨丆偡傋偰偺嶰妏宍偺撪妏偺榓偼180亱F丏傛偭偰丆愲搙偺榓傪S偲偡傞偲丆
丂丂丂360亱V=180亱F+S
偲側傞丏偙傟偐傜丆
丂丂丂S=360亱V-180亱F
丂丂丂丂=360亱(E-F+2)-180亱F
丂丂丂丂=180亱(2E-3F)+720亱
丂丂丂丂=720亱
埲忋傛傝丆愲搙偺榓偼 偱偁傞偙偲偑帵偝傟偨丏
仭仭仭丂偍傢傝偵丂仭仭仭
丂偙偺尨峞傪彂偄偰偄傞偲偒丆朻摢偺S愭惗偼島廗偺恀偭嵟拞偱偁傞丏S愭惗偺庼嬈偼偄偮傕擬偄丏恖偼擬偔側傞偲儃乕偭偲偟丆嫊傠偵側傝巚峫偑掅壓偡傞傕偺偩丏偡傞偲丆崰崌傪尒寁傜偭偰偄傞偐偺傛偆偵S愭惗偺煭棊偑旘傇丏懎偵偄偆丆僆儎僕僊儍僌偱偁傞丏僕儍僽丆傾僢僷乕丆僩儕僾儖僋儘僗僇僂儞僞乕偲捈寕傪庴偗丆惗搆偼杮摉偵姦偔側傞偲偄偆丏偙傟偑孞傝曉偟懕偔偲丆椻傗偟丆擬偟丆僒僂僫偲椻悈傪岎屳偵梺傃傞傛偆偵寣塼偺弞娐偑懀偝傟擼偺摥偒偑妶惈壔偡傞偺偱偁傞丏S愭惗偺廃傝偺僆乕儘儔偼丆乽椻偊乿偱偼側偔丆庼嬈傪妝偟偔丆柺敀偔墘弌偡傞乽嶀偊乿偱偁傝丆柍岥側巹偼丆偦偺榖弍偵偄偮傕懜宧偺擮傪書偄偰偄傞丏傕偪傠傫丆偲偒偍傝僊儍僌傪杮摉偵偼偢偟偰偟傑偄丆廃傝偼暵岥偡傞偑丆偦傟傕傑偨怱偺抔偐偝偺敪業側偺偱偁傞丏
丂偦偺俽愭惗偐傜丆崱夞乽懡柺懱偺怓暘偗乿偲偄偆嵟忋偺僾儗僛儞僩傪偄偨偩偄偨丏偄偮傕愭惗偺傾僀僨傾偵憡忔傝偝偣偰偄偨偩偄偰偄傞摉曽偼丆彮偟偱傕敪揥偺巺岥傪採嫙偱偒傟偽偲巚偄丆儗億乕僩偲偟偰傑偲傔偝偣偰偄偨偩偄偨丏
丂偲偙傠偱丆懡柺懱偺柌偺峀偑傝偼傑偩傑偩懕偔丏
丂嘆懡柺懱偺椬傝崌偆柺偺怓傪堎側傞傛偆偵揾傝偲偒丆嵟掅壗怓偁傟偽偄偄偩傠偆(嬻娫偺係怓栤戣偱偁傞)
丂嘇懡柺懱傪揥奐偟偨偲偒丆偦偺揥奐曽朄偼壗捠傝偁傞偩傠偆
丂揾傝暘偗偩偗峫偊偰傕儚僋儚僋偡傞傛偆側柺敀偄栤戣偑偱偒偦偆偱偁傞丏偙偺屻丆偝傜偵憡忔傝偟偰偄偨偩偗傞曽偑偱偰偔傞偙偲傪愗朷偡傞傕偺偱偁傞丏
仸杮儗億乕僩傪嶌惉偡傞偵偁偨傝丆墦嶳孾愭惗偺挊彂媦傃丆摉曽偺昻庛側俁俢僀儊乕僕傪曗偄丆懡柺懱偺恾傪昤偔偨傔偵RapidLapin巵偺懡柺懱昤夋僜僼僩傪棙梡偝偣偰偄偨偩偒傑偟偨
丂仜嶲峫暥專丂丂悢妛偺峀応乽俁師尦偺悽奅乿丂墦嶳孾挊丂傎傞傉弌斉姧
丂仜巊梡僜僼僩柤丂UniformPolyhedronBuilder ver0.01丂(挊嶌尃幰RapidLapin)




 丂摨條偵掙柺傪敳偔偲丆偙偺応崌偼塃恾偺傛偆側晽幵偺宍偵揥奐偝傟傞丏偙偺恾偱偼丆拞墰偺嶰妏宍偺奜懁偵俇偮偺嶰妏宍偑攝楍偝傟偰偄傞傛偆偵尒偊傞偑丆偙傟偑岆偭偨夝朄偺梫場偲側傞丏拞墰偺嶰妏宍偵懕偒丆奜懁偺俇偮偺嶰妏宍傪揾偭偰偄偔偲丆
丂摨條偵掙柺傪敳偔偲丆偙偺応崌偼塃恾偺傛偆側晽幵偺宍偵揥奐偝傟傞丏偙偺恾偱偼丆拞墰偺嶰妏宍偺奜懁偵俇偮偺嶰妏宍偑攝楍偝傟偰偄傞傛偆偵尒偊傞偑丆偙傟偑岆偭偨夝朄偺梫場偲側傞丏拞墰偺嶰妏宍偵懕偒丆奜懁偺俇偮偺嶰妏宍傪揾偭偰偄偔偲丆







 丂惓懡柺懱偺僇僪(捀揰)傪偦偓棊偲偡偲怴偨側棫懱偑弌尰偡傞丏椺偊偽惓巐柺懱偺係偮偺捀揰傪曈偺嶰摍暘揰偱愗傝棊偲偡偲丆惓嶰妏宍偺愗傝岥偑係偮偱偒丆惓巐柺懱偺柺偺悢(係)偩偗惓榋妏宍偑嶌傜傟傞丏偲偙傠偱丆偙偺棫懱偺奺捀揰偺廃傝偺懡妏宍偺攝楍傪傒傞偲丆傒側摍偟偔塃恾偺傛偆偵攝抲偝傟偰偄傞偙偲偑暘偐傞丏
丂惓懡柺懱偺僇僪(捀揰)傪偦偓棊偲偡偲怴偨側棫懱偑弌尰偡傞丏椺偊偽惓巐柺懱偺係偮偺捀揰傪曈偺嶰摍暘揰偱愗傝棊偲偡偲丆惓嶰妏宍偺愗傝岥偑係偮偱偒丆惓巐柺懱偺柺偺悢(係)偩偗惓榋妏宍偑嶌傜傟傞丏偲偙傠偱丆偙偺棫懱偺奺捀揰偺廃傝偺懡妏宍偺攝楍傪傒傞偲丆傒側摍偟偔塃恾偺傛偆偵攝抲偝傟偰偄傞偙偲偑暘偐傞丏
 丂掙柺傪屌掕偟偰揾偭偰傒傛偆丏柺悢偼丆傕偲偺惓懡柺懱偺捀揰悢+柺悢偱偁傞偐傜俉怓偱揾傝暘偗傞偙偲偵側傞丏掙柺傪惓嶰妏宍偲偡傞偲丆俁偮偺惓屲妏宍偑曈傪嫟桳偡傞偙偲丆媦傃惓嶰妏宍偺屄悢偑俆屄偱偁傞偙偲偐傜丆偦偺揾傝暘偗曽偼丆
丂掙柺傪屌掕偟偰揾偭偰傒傛偆丏柺悢偼丆傕偲偺惓懡柺懱偺捀揰悢+柺悢偱偁傞偐傜俉怓偱揾傝暘偗傞偙偲偵側傞丏掙柺傪惓嶰妏宍偲偡傞偲丆俁偮偺惓屲妏宍偑曈傪嫟桳偡傞偙偲丆媦傃惓嶰妏宍偺屄悢偑俆屄偱偁傞偙偲偐傜丆偦偺揾傝暘偗曽偼丆 丂棫曽懱偺僇僪傪曈偺拞揰偱愗傝庢傞偲弌棃忋偑傞丏偁傞偄偼丆惓敧柺懱偺曈偺拞揰傪愗偭偰僇僪傪偲偭偰傕偱偒傞偐傜丆偙偺柤傪姤偡傞丏塃恾偐傜暘傞傛偆偵丆惓嶰妏宍俉屄偲惓曽宍俇屄偐傜峔惉偝傟傞丏柺傪屌掕偟偰揾傝暘偗傪峫偊傞偲丆偦偺柺偺宍偵傛傝師偺俀捠傝偺寁嶼偑峫偊傜傟傞丏
丂棫曽懱偺僇僪傪曈偺拞揰偱愗傝庢傞偲弌棃忋偑傞丏偁傞偄偼丆惓敧柺懱偺曈偺拞揰傪愗偭偰僇僪傪偲偭偰傕偱偒傞偐傜丆偙偺柤傪姤偡傞丏塃恾偐傜暘傞傛偆偵丆惓嶰妏宍俉屄偲惓曽宍俇屄偐傜峔惉偝傟傞丏柺傪屌掕偟偰揾傝暘偗傪峫偊傞偲丆偦偺柺偺宍偵傛傝師偺俀捠傝偺寁嶼偑峫偊傜傟傞丏


 丂惓懡柺懱丒弨惓懡柺懱偼偲傕偵丆乽偡傋偰偺捀揰偺廃傝偺攝楍偑摍偟偄乿懡柺懱偱偁傞偐傜丆偦偺攝楍傪傒傞偙偲偱丆傕偲偺懡柺懱傪梊憐偡傞偙偲偑偱偒傞丏
丂惓懡柺懱丒弨惓懡柺懱偼偲傕偵丆乽偡傋偰偺捀揰偺廃傝偺攝楍偑摍偟偄乿懡柺懱偱偁傞偐傜丆偦偺攝楍傪傒傞偙偲偱丆傕偲偺懡柺懱傪梊憐偡傞偙偲偑偱偒傞丏

