ポアロ完結編です。

　この小説はもともとは、ある研究レポートのあとがきとして書いたものなのですが、いつのまにか独立した一つの教育論として発表することになってしまいました。その後、ネット上で「数学と教育」の距離を論議する問題が生じ、それを受ける形で第２章が執筆されたのですが、不用意にもその発表の場で第３章を計画しているといってしまったために、引くに引かれず、５年の歳月を経て完結編をまとめるハメになりました(５年もかかって執筆したわけではなく、なにせ性格がルーズでいい加減なものですから、書くぞ！という強い意志が……。実はモノトーン・ビジョンから考えると２０年経ってしまいました。その間に４つの学校に勤務し、それぞれの職場で結果としては１編ずつ書いたことになります)。なお、この辺の経緯については、第１章・第２章のあとがきとして書いたものを載せましたので、ご参考ください。

　さて、第３章は、ホームズの目を通して語られています。しかしホームズが主人公というわけではありません。主演はやはりポアロに設定してあります。ポアロの人物像・理念を第３者がみたらどうかということで、対極にあるようなキャラクターの目を通して話を進めたかったのです。結果、執筆側も随分ホームズの教育観に影響を受けてしまいました(書き始めはそんなことは考えてもいなかったのですが)。たぶん、第２章で登場したマープルの視点で書いたらまた違った教育論が見えてくるかもしれません(あっ、書きませんよ、第４章は……)。要は、それだけ教育は不安定(不完全ではありません)なものだということなのです。まあ、その対象が人間なのだから、人間が人間を分析するという自己矛盾(パラドックス)を抱える以上、当然なのかもしれませんが。

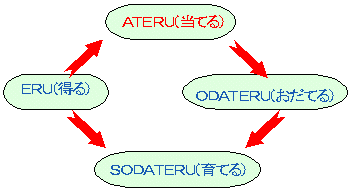
　ところで、ホームズの教育と数学のスタンスは、みなさんはどうお考えでしょうか。文中ではホームズがポアロについては教育寄りであると指摘しますが、自身については語りません。実は、ホームズも教育により近い立場にあるといえます。文中、ポアロの公開授業においてもホームズが思索している内容は教育論そのものなのです。このように、お互い近い立場にいながら対極に位置しているのは、教育は直線的な土台で判断すべきではなく、平面的(多面的)に議論する必要があることを意味します。不安定であると前述した理由はそこにあるのです。例えば、本文のＴＳＴについては、

と、ＡＴＥＲＵから出発し、ポアロとホームズは両極方向に指導を展開する解釈をしています。しかしこれを平面的に考えるならば、右表のように、「当てる」ことから「得る」ことを最終目標に設定することも可能となり、ホームズとポアロの教育論はずいぶん近づくことになります。

　ひょっとしたら、同僚であるミス・マープルならば喧嘩ばかりをしている二人の仲をとりもとうとして、このような発想をするかもしれません(あっ、書きませんよ、第４章は)。もっとも、ポアロは納得するでしょうが、ホームズはさらに結論が冗長に過ぎると文句はいうでしょうが。そして間にはいったマープルは、ホームズに理解してもらうために空間的思考にまで広げて解釈をし、そのうちにホームズを妙に意識するようになり……(あっ、書きませんよ、第４章は)。

　これは視覚認識でいえばモノトーン・ビジョンにおける、虫観、鳥瞰ということになります。では土竜感はというと、精神面の内的空間の世界です。そしてこの空間の中にきっと、教育を安定化させる要素が存在しているのでしょう。

　それは、ごくありふれた、誰もが知っている、そして持っている、単純なモノなのかもしれません。

２００２．３．１２

【第１章あとがき】

　推理小説と数学を比較してその解法論を、と企てて話を進めているうちに、とんでもない方向へと展開してしまいました。でも、「分かる」ということは、教育の永遠のテーマでしょうから、これはこれで良かったと思います。なお、方向がずれてしまったために触れられなくなった、多面的思考に関してひとつ。

　刑法の緊急避難の問題に、「カルネアデスの舟板」というのがあります。これは、船が難破して、二人の乗組員が海に投げ出されたとします。二人は必死でちょうど流れてきた小さな板につかまろうとしますが、二人でつかむと板はその重さに耐えきれず沈んでしまいます。結局、二人は板の奪合いをして、一人が助かり、一人が溺れ死ぬということになります。この場合、助かった人は、殺人をしたことになりますが、これを刑法では、緊急避難といって、無罪とみなします。

　ところで、この話を聞いていた子供が次のようなことをいったそうです。

　「可笑しいの。ふたりが交替で、立ち泳ぎをしたら、二人とも助かるのに」

　こういう発想、大事にできたらと思います。

１９９２．１．１０

　この後、ポアロの授業がうまくいっているわけではけっしてありません。教育とは解決されない問題なのであり、解決されることはきっと教育の死を意味するのでしょう。この文章を書いたわたしでさえ、ポアロに対する反論は山ほどあります。常に矛盾と問題を抱え、生徒と対峙し悩んでいます。教育を実践するそれぞれの環境においては何が正しいのかその判断は、その中で苦悩する個々の教師に委ねられます。教師はもっと教育を見ることに慎重であらねばならないのでしょう。

　こんな言葉があります。

　　「花を見ている。花も見ている。」

　花を生徒に置き換えて下さい。

１９９５．８．３１

　このレポートは未完成です。第１章、第２章に続いて最終章としての第３章を考えていたのですが、ちょっとした事情で今回発表させていただくことにしました。

　もともと本レポートは、各章とも独立した形で過去に発表したものです。第１章は、平面幾何に関するレポートのあとがきを幾何と推理小説とを比較しながらまとめようとしていたとき、文章を打っているうちに思わぬ方向に話が進んでしまい、それならばということで、別レポートとして発表しました。したがって、第１章の途中から急にポアロなる架空の教師が主人公として登場し、ポアロの呟きで物語が展開します。しかし、当初予定していた話から外れてしまったため、消化不良で終わる結果となりました。

　そこで、それを補うために第２章が書かれました。「カルネアデスの舟板」を例に挙げて、教育というものは実に不安定でかつ流動的なものであるかを投げかけてみました。人間の心が不変でない以上、教育やその価値も不変であるとは思えないのです。なお、この章では新しく２人の架空の教師が登場します。かなり個性的なキャラクターであるため、これで終わらせるのはもったいなくなり、第３章を書く予定でいたのです。おおかたの粗筋は考えてあるため、そのうち手が空いたらゆっくりと書こうと悠長に構えていたのですが、このレポートがどう評価されるか反応を見てみたい衝動に駆られる事件？が起きました。

　数実研のホームページ「数学のいずみ」に載っている「Ｓｈａｄｏｗ Ｌｉｎｅ」の問題が、メーリングリスト「mathedu」において問題提起として公開されたのですが、予想を上回る多くの人達の意見や質問が飛出してきました。空間や人間関係を超えて、メディアを媒介とした新しい研究討論が生まれたのです。バーチャル・コンファレンス(架空会議)と言われるこの新しい会議形態は、今後、私達の数実研の研究にも大きな影響を与えていくことでしょう。

　さて、このmatheduでの意見交換の中味については、早苗先生によるレポート発表をみていただきたのですが、ここで参加している方々が、いろいろな立場、方面の人達であることが面白いのです。もちろん数学関係者ではあるのですが、

　この、数学と教育の間の様々な人達の討論は、とても興味あるものでした。私達の研究会は、立場にしろかなり等質のメンバーにより成立していることは異論のないことでしょう。したがって、レポート発表も「暗黙のｙｅｓ」で意見がまとめられてしまうことってどうしてもあるかと思います。共通理解という長所の反面、それはよどみを生み、研究会の活性化が失われる危険性につながります。そういう危惧を日頃感じていたこともあり、このmatheduでの討論は、衝撃的なものでありました。

　今回の問題についていうと、２円の交点を通る直線の存在性から始まり、やがては、教育論にまで発展してしまいます。「受験数学」とその「弊害」、我々が日常現場で悩んでいることが、違う立場の人から語られることは新鮮であり、嬉しいものでした。 ところで、私達のレポートは、生徒という対象がある以上、「数学教育者」という観点で書かれることが多いかと思いますが、それがかえって私達の研究内容を狭めてしまっているようにこのmatheduでの討論を通して感じたのです。

　もっと数学と教育の間の幅がある研究があってもよいのでは。

　それが、本レポートを未完成の段階で発表する理由です。このレポートは、思いっきり教育の側に傾いている内容となっています。「数学のいずみ」が、他階層の人達を将来的にターゲットにし、広く教育に携わる人達、そうでない人達にも意見を求めていこうとするならば、こんなレポートがあったっていいのでないかと思うのです。この物語の中でポアロがとる行動は、理解が得られるでしょうか。それとも非難されるでしょうか。そう考えると楽しくもあります。第３章の構想は既にできあがっていると前述しましたが、このレポートに対する意見によってはその内容は変わってしまうかもしれません。

　あなたはどんな意見をお持ちですか。

　どうぞ、ポアロを育ててください。

１９９８．７．１４