丂埲慜丄悢幚尋偱廳暋慻崌偣偺巜摫偺堦椺傪丄儗億乕僩偲偟偰傑偲傔敪昞偟偨偙偲偑偁傝傑偡(乽悢妛偺偄偢傒乿偺拞偵廂傔傜傟偰偄傞偲巚偄傑偡偑)丅摨師愊偲傒傞偺偱偼側偔丄慻崌偣偺墳梡偲懆偊偰
丂偲偙傠偱丄偙偺撪梕偵偮偄偰丄屻偵悰尨愭惗(憯娾崅峑)偲悢幚尋偺崸恊夛偱巐曽嶳択媊傪偟偰偄偨偲偒偵丄愭惗偐傜丄乽宱楬偲偟偰峫偊傞曽朄傕偁傝傑偡偹乿偲巜揈偝傟偨偙偲偑偁傝傑偡丅嵟抁宱楬栤戣偼丄慻崌偣偺戙昞揑側傕偺偱偡偑丄偦傕偦傕嵟抁宱楬偺栤戣傪廳暋慻崌偣偺掕媊偲偟偰愢柧偟偰偄傞俽幮偺嶲峫彂傕偁傝傑偡偐傜丄偙傟傪怗傟側偄偺偼傗偼傝曅庤棊偪偱偟偨丅幚偼儗億乕僩傪傑偲傔偨偲偒偼乽暲傋曽乿偺曽朄偍傛傃乽婎弨悢乿偺媮傔曽偵榑揰傪抲偄偰偟傑偭偨偨傔偵丄宱楬偵傛傞曽朄偼傑偭偨偔摢偺拞偵巚偄偮偐側偐偭偨偺偱偡丅
丂偟偐偟丄幚嵺偵儗億乕僩撪梕傪幚慔偵堏偟偰偄偔偲丄乽巇愗傝暘攝朄乿偱偼埖偄擄偄栤戣偵捈柺偟偰偟傑偄傑偟偨丅傕偲傕偲丄廳暋慻崌偣偺栤戣偼丄乽偳偆偄偭偨栤戣偑廳暋慻崌偣側偺偐乿偲偄偆偙偲偺敾抐偑堄奜偲擄偟偄傕偺偱偡丅偦偙偱尨揰偵栠偭偰峫偊偰傒傞偲丄宱楬栤戣偲偟偰懆偊傞偲悘暘偡偭偒傝偲傑偲傔傜傟傞偙偲偑暘偐傝傑偟偨丅
丂偦偙偱丄廳暋慻崌偣偺係斣栚偺巜摫朄偲偟偰丄師偺乽朹僌儔僼暘攝朄乿偵偮偄偰峫偊偰傒傑偡丅
![]() 朹僌儔僼暘攝朄
朹僌儔僼暘攝朄
| 倕倶乯俇屄偺椦岀傪俙,俛,C俁恖偵暘攝偡傞曽朄偼壗捠傝偐丅 |
丂慜夞偲摨偠栤戣偱峫偊偰傒傑偟傚偆丅
丂偝偰丄俁恖偵攝傞椦岀傪恾侾偺傛偆偵朹僌儔僼偲偟偰暘偗偰傒傑偟傚偆丅恾偼丄俙丆俛丆俠偵偦傟偧傟俀屄丆侾屄丆俁屄偲暘偗傞応崌偱偡丅師偵恾俀偺傛偆偵丄椦岀傪偢傜偟偰傒傑偟傚偆丅
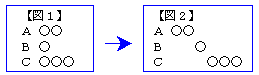
丂偙偺朹僌儔僼傪師偺傛偆偵儌僨儖壔偟傑偡丅
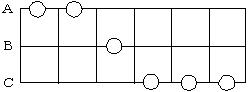
丂寢嬊丄椦岀偺暘偗曽偼丄壓恾偺揰俹偐傜揰俻傊偺嵟抁宱楬偲側傞偙偲偑暘偐傝傑偡丅
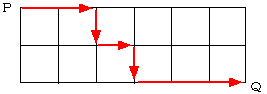
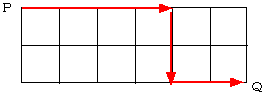 丂埲忋傛傝丄8俠2=28 (捠傝)偲側傝傑偡丅
丂埲忋傛傝丄8俠2=28 (捠傝)偲側傝傑偡丅
丂傕偪傠傫丄偙偺応崌偺嵟掅暘攝屄悢偼侽屄偲側傞偙偲偼丄俙,B,C偑偦傟偧傟係屄,侽屄,俀屄偺応崌偼塃恾偺傛偆偵峫偊傟偽偄偄偙偲偐傜暘偐傝傑偡丅
![]() 朹僌儔僼暘攝朄偐傜宱楬暘攝朄傊
朹僌儔僼暘攝朄偐傜宱楬暘攝朄傊
丂偙偺暘攝朄偼丄慜夞偺嘆乣嘊偑侾師尦揑暘攝朄偱偁傞偺偵懳偟丄俀師尦揑暘攝朄偲傒傞偙偲偑偱偒傑偡丅廳暋慻崌偣偺戙昞椺偲偟偰丄柍婰柤搳昜偺栤戣偑偁傝傑偡偑丄乽侾侽恖偺慖嫇恖偑丄係柤偺岓曗幰偵柍婰柤偱搳昜偡傞曽朄偼壗捠傝偐乿傪丄廲偵岓曗幰係柤偺柤慜傪暲傋丄摼昜悢傪朹僌儔僼偱昞偟偰傒傞偲暘偐傝堈偔側傝傑偡丅宱楬偺廲慄丄墶慄偼丄屄悢偲恖悢偲偄偆堎側傞梫慺偲傒偨俀師尦揑攝楍偲懆偊傟偽傛偄偺偱偡丅偦偟偰丄偙偺攝楍偐傜偼丄屄悢偺嵟揔壔偑廮擃偵埖偆偙偲偑壜擻偲側傝傑偡丅
俤倶)丂倶亄倷亄倸亖俉傪枮偨偡惍悢夝乮倶丄倷丄倸乯偺屄悢傪師偺応崌偵偮偄偰媮傔傛丅
|
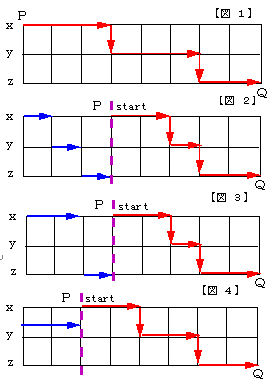 夝乯
夝乯
丂傛偭偰丄俈俠俀=俀侾捠傝丅
丂偲偙傠偱丄(2)偺愝栤偼丄恾傪傒傞偲昁偢偟傕
丂丂丂丂倶亞侾丆倷亞侾丆倸亞侾
偱偁傞昁梫偼側偄偙偲偑暘偐傝傑偡丅
丂丂丂丂倶亞俀丆倷亞侽丆倸亞侾
偱偁偭偰傕弌敪揰偵曄傢傝偼側偄偺偱偡丅(恾俁)
丂堦斒偵
丂丂丂丂倶亞倎丆倷亞倐丆倸亞們
偺応崌偼丄倎亄倐亄們偩偗start抧揰傪塃偵偢傜偣偽偄偄栿偱偡丅
偱偁傞偐傜丄塃偵俀偩偗start抧揰傪偢傜偣偽丄
丂丂丂丂俉俠俀亖俀俉捠傝
偲側傝傑偡丅(恾係)
![]() 傑偲傔
傑偲傔
|
丂奺崁偑丄侾丆俀丆俁丆係偺偳傟偐偱偁傞俆屄偺悢偺楍乮倎侾丆倎俀丆倎俁丆倎係丆倎俆乯偱 丂丂丂倎侾亝倎俀亝倎俁亝倎係亝倎俆偱偁傞傕偺偺屄悢傪媮傔傛丅 |
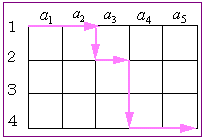 丂偙偺栤戣偵懳偟偰丄娵朹暘攝朄傗巇愗傝暘攝朄傪巊偍偆偲偡傞偲(晄壜擻偱偼側偄偱偡偑)柍棟偑偁傝傑偡丅傕偲傕偲娵朹傗巇愗傝偼乽傕偺傪暲傋偰乿偲偄偆栤戣傊偺懳張偺巇曽偱偡偐傜丄偙偺栤戣偺傛偆偵廳暋慻崌偣偺梫揰傪偢偽傝栤偄妡偗傞傛偆側傕偺偵偼懳墳偟擄偄偺偱偡丅偦偆偡傞偲弴彉慻暘攝朄偲偄偆偙偲偵側偭偰偟傑偄傑偡偑丄偙偺曽朄偑棟夝偟偵偔偄偺偼慜夞偺儗億乕僩偺捠傝偱偡丅
丂偙偺栤戣偵懳偟偰丄娵朹暘攝朄傗巇愗傝暘攝朄傪巊偍偆偲偡傞偲(晄壜擻偱偼側偄偱偡偑)柍棟偑偁傝傑偡丅傕偲傕偲娵朹傗巇愗傝偼乽傕偺傪暲傋偰乿偲偄偆栤戣傊偺懳張偺巇曽偱偡偐傜丄偙偺栤戣偺傛偆偵廳暋慻崌偣偺梫揰傪偢偽傝栤偄妡偗傞傛偆側傕偺偵偼懳墳偟擄偄偺偱偡丅偦偆偡傞偲弴彉慻暘攝朄偲偄偆偙偲偵側偭偰偟傑偄傑偡偑丄偙偺曽朄偑棟夝偟偵偔偄偺偼慜夞偺儗億乕僩偺捠傝偱偡丅
丂偲偙傠偑丄偙傟傜偺暘攝朄偵懳偟偰丄朹僌儔僼暘攝朄偼丄
傪偲偭偰偄偗偽丄梕堈偵慖傃曽傪帇妎壔偱偒傑偡丅偙偺栤偄偺応崌偼丄
丂丂丂丂俉俠俁亖俆俇捠傝
偲側傝傑偡丅偙偺傛偆偵棟憐揑側儌僨儖壔偑偱偒傞偺偼丄乽嵟抁宱楬栤戣乿偑傕偲傕偲偼廳暋慻崌偣偺栤戣偱偁傞偐傜偱偡丅捠忢偼丄偙偺庬偺栤戣偼嫵壢彂偱偼摨偠傕偺傪娷傓弴楍偱埖傢傟丄偝傜偵廲偲墶偺慖傃曽偲傒偰慻崌偣偲偟偰媮傔傞乮儓僞儓僞朄偲屇偽傟傞曽朄偱乯偺偑堦斒揑偱偟傚偆丅
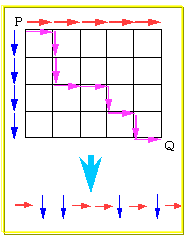 丂塃恾偺傛偆側応崌偵偼丄
丂塃恾偺傛偆側応崌偵偼丄
丂丂丂丂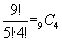
偲側傝傑偡偑丄偙傟傪丄俆偮偺墶慄傪廳暋傪嫋偟偰丄俆屄偲傞偲尒傟偽丄
丂丂丂丂俆俫俆亖俋俠俆
偱摼傜傟傞偙偲偑傢偐傝傑偡丅
丂偨偩偄偒側傝嵟抁宱楬偵寢傃晅偗偰偟傑偆偲丄巜摫偺棳傟偲偟偰崿棎傪婲偙偡婋尟惈偼偁傞偱偟傚偆丅偦偙偱丄傕偭偲尰幚揑偵屄乆偺梫慺偺(惉愌)傪愊傒忋偘偨朹僌儔僼偲傒偰儌僨儖壔傪偡傞偲丄棟夝偑梕堈偵側傞偺偱偼側偄偱偟傚偆偐丅