あとがき素朴な疑問が始まりだった。
「円から円を引くとどうなるんだろう？」
今年の数実践研夏期セミナ－の後半は，小樽桜陽高校から会場を祝津の旅館に移して，懇親会を兼ねての研究会となったが，菅原先生（札幌藻岩高校）と数学談義に花を咲かせている中で，このことが話題にあがった。数Ⅱの円と直線分野の演習で，2円の交点を通る直線（交線）を生徒に求めさせると，交点の存在を確認をしないで安易に2円の差をとってしまう生徒が多い。差をとって何も式がでないのならいいが，交点がなくても，直線の式が作られてしまう。では，この直線って何なんだろう。
そういわれてみれば，なるほどというか，なんというか，とにかく返答に窮してしまった。2人の一致した点は，たぶんその直線は，「虚円」に関係しているのではないかということであった。
2円を方程式と捉えてその解を求めるならば，その計算過程として（連立方程式の解法の鉄則，次数を下げろ）2次の項の消去が考えられ，1次式が作られる。それを円の方程式に代入することで，たとえばyが消去され，xの2次方程式の解は当然，虚数解となる。よって，1次式は，虚数点という存在しない2点を通る直線とみれるのである。
一般に2円の交点を通る曲線群は，円または直線であるからその交点が，虚数点ならば，虚円または虚数直線となるだろう。なんとなく，漠然とながら，実数平面の上を，嘲笑気味に飛び交う虚円のイメ－ジが浮かび上がったが，なんか，きもい（気持ち悪い）。もっとすんなりと説明できないものなのだろうか。と考えているうちに夜も更けてしまった（ひょっとしたら夜が明けていたかもしれないが記憶が定かでない……）。
早速，家に帰ってから「関数ラボ」でシミュレ－トしてみた（このソフトは，こういうときに思考のイメ－ジ不足を最大限補ってくれる）。だが，2円とその交点を通る曲線をパラメ－タで変化させてみたが，イメ－ジが湧かない。どう発展させればいいのだろう…………？頭を抱える。
そうした紆余曲線の末，本レポ－トは出来上がった。しかし，その結論は，相変わらず「きもい」のである。問題解決のベクトルが定まらないから観点がころころと変わり，どれひとつとっても満足いく説明にはなっていない。すべての結果が舟を漕ぎ出した後の座礁のなれの果てである。
なぜなら，この問題は2円に限定されるべきではなく，一般に2つの曲線の交点を通る曲線群の問題とみるべきなのである。2円について一応，誤魔化し的な説得調の説明をつけたところで，一般化ができなければ意味がない。たとえば，放物線 f(x，y)＝ax2＋bx＋c－y＝0 と直線 g(x，y)＝px＋qy＋r＝0から作られる曲線 kf(x，y)＋lg(x，y)＝0はどんな曲線になるだろう。放物線と直線が，2点で交わる場合，接する場合，交わらない場合と，その興味は尽きない。
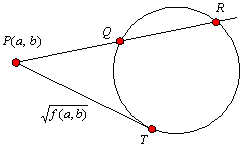だが，面白い収穫もあった。円：f(x，y)＝x2＋y2＋px＋qy＋r=0 に適当な点P(a，b)を代入すると，その値の符号により，点Pが円の内部，周上，外部のいずれかにあるかの判定がされ，
f(x，y)<0といった不等式の表す領域を求めることが可能となるがf(a，b)の値そのものが何を意味するのかということについてはいままで考えたこともない。方べきの定理自体が，単に相似な三角形から得られる相似比ぐらいに思っていたし，何故「方べき」という名を冠するのかということは気にも留めたことがなかった。それが，f(a，b)の値の意味を捉えて臨めば，思いもよらない軌跡が見えてくるのである。
だが，何よりの収穫は，この問題に出会えたということであると思っている。
それは，研究会の中で，菅原先生の提言による，「アイデアの相乗り」という発想につながる。我々がこの研究会の今後を見通せば，個々の教師がもっているアイデアには限界があるわけだから，その枯渇は，研究会の終焉を予測させてしまう。提供だけのアイデアでは続かないのである。だからこその相乗りであろう。一人のアイデアを研究会に参加する人達が発展，応用させていく。一人の疑問をみんなが共有し，解決していく（なんか学級の経営方針みたいではあるが）。こうした「ともに考える」双方向性を持った研究会でなければやがては存続の意義さえ失いかねないと危惧するのである。
だが，この交線問題も，やがて時が解決し，きっと「きもい」感情を拭い去ってくれるに違いない。