Ｓｈａｄｏｗ　Ｌｉｎｅ ・・・再び

円束問題は，

ベキの比としての点の軌跡
球束とxy平面との交わりが作る曲線

　だが，それは，せっかくの円束のもつ神秘的なイメ−ジを破壊してしまうことにもなる。

　曲線：x²＋y²＝dは，d＞0 のとき，半径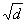の円を表すが，d→0とすると，点円に収束し，さらに，d→−∞とすると，虚平面（複素平面ではない）に半径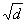の円が広がっていく。

　円の中心という，実世界と虚世界を隔てる出入り口に，次第に円が吸い込まれていき，その後に虚世界の中で，同心円を描きながら円が膨らんでいく。この様はワクワクする想像力を掻き立てるものである。x²＋y²＝−1は，半径iの大きさ1の円であるというイメ−ジは大切にしたいと思うのである。

では，虚円は，具現化できないものなのであろうか。実円は，xy平面上の点のプロットとして描かれるわけであるから，点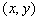を複素数の組と考えれば，新たに2つの次元を構築しなければならない。

　よって，虚円の世界は，想像の束縛から逃れることはできないのである。だが，x，yのどちらか一方のみを複素数と考えれば，ほんの少しの部分は覗くことができる。

　交わらない2円を

　　C₁：x²＋y²＝1，　　C₂： (x−3)²＋y²＝1

とする。方程式が虚数解についても満たすと考えてみよう。xは実数，yは複素数とし，

　　y=u+vi　(u∈R，v∈R)

とおく。 C₁ に代入すると，

　　x²+(u+vi)²＝1，　(x²+u²−v²)+2uvi=1

　　　　∴ 　x²+u²−v²=1，2uv＝0

　　u＝0のとき，x²−v²＝1（双曲線）
　　v＝0のとき，x²＋u²＝1（円）

となる。

　同様に，円C₂について考えると，(x−3)²＋(u＋vi)²＝1 より，

　　u＝0のとき，(x−3)²＋v²=1
　　v＝0のとき，(x−3)²＋u²=1

を得る。

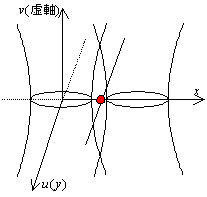
　よって，右図のように，虚軸であるv軸を立てれば，xy（xu）平面上にはもともとの2円であるC₁，C₂が描かれるが，yが虚数であるときには，xv複素平面上に，双曲線が広がっていく。その双曲線の交点の影が，x軸上に，2円の差として作られる直線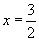の一部として，浮かび上がってくる。

　少しは，影としての直線を与える「虚円」が存在している，虚空間の入り口が垣間見れたのではないだろうか。

　チョッキのポッケから取り出した時計を見ながら走っていく兎を追って，垣の下の兎穴に落ちたアリス。どこまでも落ちていく自分に彼女はこう語りかける。

　「わたし地球の向こうへ抜けちゃうのかしら。さかだちして歩いている人たちの中に出ていったら 面白いわね！。反感地っていったかしら……」