Ｐｒｏｊｅｃｔｉｏｎ　Ｌｉｎｅ （射影として）

　その差が直線として表現される方程式のもとの2曲線（円）は，一意的に決定するわけではない。

　たとえば，

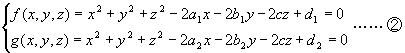
　�@，�Aともに2つの方程式の差は，同じx，yの一次式を得るが，曲線としては異なるものを意味する。�@は直線，�Aは平面である（もちろん，�@は空間図形と考えれば直線にはならないが）。

　ここで，�@と�Aの図形の関係は，�Aの表す2球面とxy平面との交わりが，�@の2円と考えればよい。さらに，�@の2円は必ずしも交わらなくとも，c→∞とし，z軸上方，無限遠点に球面の中心(a₁，b₁，c)，(a₂，b₂，c)をとれば，�Aの2球面は，交わりをもち，その交わりは円を含むxy平面に垂直な平面を作る。その平面の影（射影）が直線として，xy平面に現れると考えればよいだろう。

　したがって，�@は，�Aの，z＝0の場合である。2曲線の交点を通る曲線群についても，同様に捉えることができる。

　　　kf(x，y)＋hg(x，y)＝0　→　kf(x，y，0)＋hg(x，y，0)＝0
と同一視すれば，円束は，�Aの2球面の交わりである平面を含む球面とxy平面との交わりにできる円とみなせばよいことがわかる。