点円・虚円

　曲線 C：x²＋y²−2ax−2by＋d＝0は，(x−a)²＋(y−b)²＝a²＋b²−d より，d＜a²＋b²のとき，円を表し，d＝a²＋b²のときは点（円）となる。さらに，d＞a²＋b²のときは虚円を表し，完全に実数平面上から姿を消してしまう。この虚円を，視覚化してみよう。

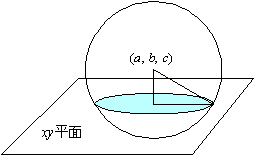　S： f(x，y，z)＝x²＋y²＋z²−2ax−2by−2cz＋d＝0とする。一般形に変形すると，この方程式は，

　　(x−a)²＋(y−b)²＋(z−c)²＝a²＋b²＋c²−d

であるから，d＜a²＋b²＋c²であるように，十分大きな値cをとると，

　　　中心(a，b，c)，半径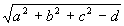

の球面となる。この球面とxy座標平面との交わりであるf(x，y，0)＝0が曲線Cの方程式を表すと考えればよい。すなわち，点円は，球面Sとxy平面が接することであり，虚円は，xy平面上方に球面Sが浮かんでいる状態を示すわけである。