べきと根軸

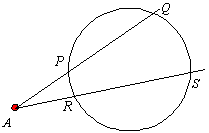
方べきの定理 定点Aから定円に引いた2直線が，定円と交わる点を それぞれP，Q，R，Sとするとき， 　　　　AP・AQ＝AR・AS が成り立つ。

　初等幾何の代表的な定理であり，三角形APRと三角形ASQが相似であることを利用すると簡単に証明できるが，この定理の本質は，

　　定点Aを通る直線が定円と異なる2点P，Qで交わるとき，AP・AQ＝一定

であるということである。実際，2点R，Sを点Pから円に引いた接線の接点Tに限りなく近づけていけば，AP・AQ＝AT² となることから予想される（証明は接弦定理による）。では，その一定数AT²を求めてみよう。

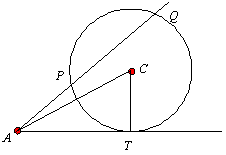
　定点A(x₀，y₀)，定円 f(x，y)＝(x−a)²＋(y−b)²−r²＝0（円の中心はC(a，b)とする）とおくと，

　　　AT²＝AC²−CT²＝(x₀−a)²＋(y₀−b)²−r²＝f(x₀，y₀)

となる。

Ｎｏtｅ）

　方べきの定理は，円の内部の定点についても成立する（証明は三角形の相似関係より）。このときのAP･AQの値は次のように計算する。

　円の方程式を f(x，y)＝x²＋y²＋ax＋by＋c＝0 とおき，定直線を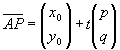 とする。

　x＝x₀＋tp，y＝y₀＋tqを円の方程式に代入して，

　　　(x₀＋tp)²＋(y₀＋tq)²＋a(x₀＋tp)＋b(y₀＋tq)＋c＝0

　　　(p²＋q²)t²＋(2px₀＋2qy₀＋ap＋bq)t＋(x₀²＋y₀²＋ax₀＋by₀＋c)＝0

　この2次方程式の2解が，円と直線の交点P，Qであるから，解と係数の関係より，

　　　　AP･AQ＝x₀²＋y₀²＋ax₀＋by₀＋c＝f(x₀，y₀)＝（一定）

となる。このとき，この一定数を定点の定円に関するベキという。

　これから，f(x₀，y₀)の値を考えれば，点Aが円の外部にあるとき， AP･AQ＞0であり，円周上の点であるとき，AP･AQ＝0，円の内部にあるときは，AP･AQ＜0である。すなわち，AP，AQは有向線分であり，円の内部に点Aがあるとき，APとAQは逆向きとなる。

　さて次に，2円

　　　C₁： f(x，y)＝x²＋y²＋ax＋by＋c＝0･･･�@
　　　C₂： g(x，y)＝x²＋y²＋px＋qy＋r＝0･･･�A

に対してベキの値が等しくなるような（接線の長さが等しい）点A(x，y)の軌跡を考えると，

　　　f(x，y)＝g(x，y)

であるから，�@−�Aから作られる直線の方程式に一致する。

　この直線を2円の根軸という。

　このように，解析幾何の観点では，�@×k−�A×h によって作られる

　　　kf(x，y)−hg(x，y)＝0･･･(*)

は2円の交点を通る曲線群(円束)とみるのではなく，f(x，y)：g(x，y)＝h：k より，ベキの比（接線の長さの平方の比）が一定である点の軌跡と考えればよい。

　この軌跡は，k=hのとき，直線（根軸）となり，k≠hのとき，円を表す。

　そして，2円�@，�Aが交わるとき，2円の交点を通る曲線群に一致するわけである。このように点の軌跡としてみれば，2円の交点の存在の有無に関わらず，(*)は意味をもってくるわけである。

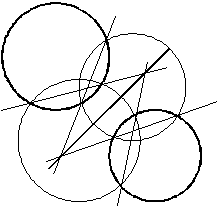Ｎｏtｅ）

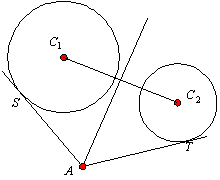
　2円が交わっているとき，根軸は，2円の交線となるが，交わらないときは，次のように求める。

　2円C₁，C₂の両方に交わるような円S₁を描き，C₁とS₁，C₂とS₁の根軸の交点を求める。次に，同様に，2円C₁，C₂の両方に交わるようなS₁とは異なる円S₂を描き，根軸の交点を求める。こうして求めた2つの交点を結ぶ直線が，C₁とC₂の根軸となる。

　だが，この考え方は問題の論旨をすりかえてしまったものである。もともとは，2円の交点を通る直線は，その方程式の差をとることで求まるものが，2円が交わらないときにも，どうしてでてくるのかということであった。曲線群としてみたときの問題は依然解決されてはいない。2円が接する場合は，交点は1つであるから，その点を通る直線は無数に存在するが，なぜそのうちの1本だけに限定されるか，また，2円が交わらないときの直線が何を表しているのか，疑問は残るのである。

　そこで，別の観点からこのことを考察してみよう。