そしてこのことは、仮想会議の弱点を暗示しています。メールに飛び込んでくる膨大な情報・意見は一方通行になりがちなのです。１つのメールの感想を考えている間に次のメールが飛び込んでくるという状態です。これを、通常形式の会議に例えるならば、開式の挨拶と同時に参加者全員から一斉に議題に対しての意見が吹き出すといったことでしょうか。メールにおいてはやはり架空会議という性格上、提案内容をお互いに咀嚼し練るといった時間が足りないのです。＜仮想会議について＞
おぼろげな存在だったShadow Line(以下S.Lと略)がずいぶん重みをもってしまったようです。
メーリングリストmatheduにおいて、S.Lについての問題が稲北高校の早苗先生によって公開提案されるやいなや、多くの方々からの質問や意見が寄せられ、ネットワーク上で、いつしかバーチャルコンファレンス（仮想会議）なる会議の形態が確立してしまいました。
日本全国をコンピュータを媒体として駆け巡ったS.Lの問題は、このレポートの作成者や提案者の思惑の枠を超えた広がりをもち始め、数学という共通言語で結ばれた見知らぬ仲間達によって分析そして再構築され、新たな課題を残して収束しました(現在までのところ）。
ところで、レポート作成者としての私はというと、インターネットに無縁な存在ゆえ、本件の感想を早苗先生に求められたので、Faxで送られてきた先生方の意見を空いた時間にでもゆっくりと拝見しようと悠長に構えていたところ、インターネット上では加速度的なスピードで議論が展開してしまいました。藻岩高校の菅原先生の「そのうち中村先生から意見発表があると思います」という催促に答えることができないうちに気がつけば蚊帳の外にいた状態です。
そしてこのことは、仮想会議の弱点を暗示しています。メールに飛び込んでくる膨大な情報・意見は一方通行になりがちなのです。１つのメールの感想を考えている間に次のメールが飛び込んでくるという状態です。これを、通常形式の会議に例えるならば、開式の挨拶と同時に参加者全員から一斉に議題に対しての意見が吹き出すといったことでしょうか。メールにおいてはやはり架空会議という性格上、提案内容をお互いに咀嚼し練るといった時間が足りないのです。
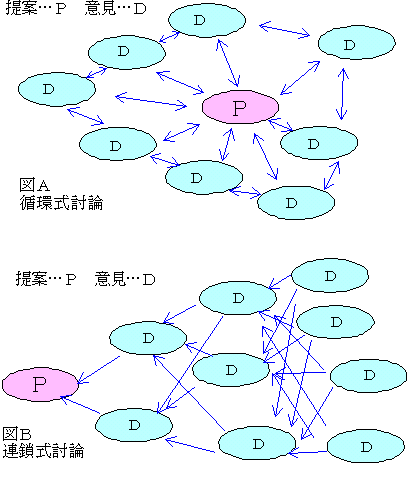
これをモデル化してみると、従来の会議形式が図Ａとなるのでしょう。一つの提案に対してお互いの意見が交換され、質的に提案の内容を充足するもの。これを循環式討論としましょう。これに対して仮想会議は、一つの提案に対しての意見がまた新たな再提案といった形で討議が展開し、どんどんと量的に提案が膨れ上がっていきます。図Ｂのこの形式を連鎖的討論と呼びましょう。各図において、矢印は意見間の同調を表わす距離(同調意見の楕円間の距離)と考えてください。そして連鎖的討論においては、矢印が一方通行であることと、同時系列の意見は反映されないことに注意してください。こうした状況で、意見という提案が膨れ上がると主提案は破棄され、会議が混乱する危険性をあわせ持っているのです。
言葉が適当ではないかもしれませんが、下手をすると、「言いたい放題」になってしまうのです。だから、未来の会議形態であるこの仮想会議をもっと質的にも向上させるには、レフリー(司会)の存在が不可欠になってくると思います。、仮想会議における仮想の運営者が選ばれ(例えば、提案者)、レフリーを常に経由しながら量的、質的に会議の運営を計り、主提案(あるいは会議上での新しい提案)の方向性を維持する必要性があるでしょう。
Matheduを始めとする仮想会議の今後を期待したいものです。
＜matheduにおけるＳ.Ｌ問題の私見＞
さて、本題のＳ.Ｌ問題についてですが、もう一度、早苗先生の提案を(私のではありません)を次に提示すると、
x2+y2=1･･････① x2+x2-6x-8y+16=0･･････②の交点を通る直線は何かというレポートの一節から、「(＊)の直線は虚数の軌跡によって作られる曲線の影のようなもの」というひとつの結論に対して「虚円のイメージ化」の可能性と必要性を問い、どう生徒に説明すべきかということでした。
という問題を、①－②より 6x+8y-17=0･･････(＊)
としてしまうのは、テクニック偏重の受験数学の弊害の最たるものである。
ところで、Ｓ.Ｌ問題に関してご意見をいただいた方は、前述の仮想会議の文章でも触れたように実にバラエティにとんだ「教育と数学の間のいろいろな立場」の先生方でしたから、いつしか問題は、「受験数学」とその「弊害」といったことにまで及び、早苗先生の提案とは大きくずれてしまったようです。そのことも含めてもう一度Ｓ.Ｌ問題とその意見を整理し、私見を述べたいと思います。Ｓ.Ｌ問題のレポートには３つの視点からの考察がされています。
そのことをお話する前にもう少し①～③の考え方についてまとめてみましょう。①は、直線の方程式を軌跡とみることで(＊)を数学的にはまったく問題のない形で説明しています。③は、複素化し(＊)の一部を覗いてみようじゃないかということで、これは此方サイドの欲求解消的な意味での説明です。②は、では仮に生徒に対して説明するとしたらどう話すのが適当だろうかという教育という立場での考察です。
①数学的、 ②教育的、 ③数学教育的
とでもなるのでしょうか。もちろん私の一番主張したかったのは②ですが、この考え方が適切であるかどうかが疑問なのです。だから②教育的考察は、その解釈を周りに委ねた形でレポートの真ん中に配し、レポート自体の結論を避けてしまったのです。そして、その疑問が「きもい」感情なのです。
では何が「きもい」のかというけっしてＳ.L問題の虚円についての説明に対してとは思っていません。その対象となるべき生徒への説明に対しての「きもさ」なのです。これが早苗先生の後半の「生徒への説明」の方法につながっていくのでしょう。
Ｓ.Ｌ問題の考察に関しては、matheduの中で多くのご意見をいただきました。
「実座標平面では交点集合は空集合であるから極端な話、どんな方程式でもOK。」
「パラメータにより交点通過の曲線群を考えて、直線となるようにパラメータを決定。」
「２円を引いて得た方程式について、十分条件としての確認をする。」
どれももっともな意見かと思います。そしてこれらのことは多分現場では指導、説明されていることでもあると思うのです。「その(虚円の)存在性を意識させる必然性はあるのか」というご意見もありました。「99％以上の生徒にはないだろう」という判断でしたが、私もそう思います。この交点通過が現場で取り上げられる状況を考えるならば、条件の中に交点の存在は保証されているはずで、交点があるという前提での発問になるはずなのです(このことのご指摘も意見の中にあったかと思います)。限られた指導の時間内で(今は週５時間しかありません)、交わらない場合を提示してあえて混乱させる必要はないでしょう。数学好きの少年達には自身の思考発達過程の中で「どうして」という疑問が沸き上がるかと思いますが大半の生徒にとっては関係のないことなのです。
ところで問題はこの関係ない生徒の層なのです。どのご意見を伺っても感じることは、ある程度数学的能力と知識を身につけた生徒の層に対しての指導法というように私は読んでしまいました。(間違っていれば申し訳ありません)
でも教育の場では数学が分からない生徒が圧倒的多数を占めているのは厳然たる事実であり、教育界ではその子らをslow learner と呼んでいます。どう訳すのでしょうか。私は slow runner というべきではないかと思っています。｢learner｣という言い方は私には理解が止まっているように聞こえるのです。でも彼らはmy paceで学んで走っているだけのことであり、それは人と比較されるべきではありません。数学が分からない子らは、思考が遅いというより、いろいろなことを思考する、すなわち思考し過ぎるからだと思うのです。彼ら自身がその思考をゆっくりと整理して解決に向えばいいのです。
だから彼らが走っている途中で躓くことは実に些細なことが多いのです。例えばこのS.L問題にしても、パラメータで表現した後、直線を表わすのはパラメータ=-－１だから、この直線が云々」と説明して結果として、「二円の差＝直線」という関係がでてしまった後、２円が離れていてもそんなことを気にしないのは案外数学のできる生徒ではないでしょうか。仮に疑問であってもmatheduの中で出されている説明で彼らは理解してしまうでしょう。先程の99％の説明の必然性のなさの中には論理的思考ができる生徒も含まれるはずだと思います。そして、slow runnerについてももちろん含まれるでしょう。
でも、slow runnerに対してこそ、もし生徒の側から質問がでたとしたら、何らかの説明が必要かと思うのです。考えが深すぎるslow runner にとっては、その思考が２円が交わっていないケースについて及んだとき、彼らは理解できないのです。幾らｘ，ｙは虚数だからと説明しても、現実にそこにｘ，ｙの一次式、すなわち直線の方程式が存在しているのですから。
だから、Ｓ.Ｌ問題はもともと２円が交わらないという条件のもとで考えているのであって、交わっている場合との比較考察(背理法的に)をするつもりはありませんでした。交わらない場合をどう解釈するかに固執したいのです。それが生徒への説明に対してまだ不十分であるからこそ「きもい」感情となっています。特に、教科書の中から空間図形の分野がほとんど消えた現状では、なおさら「きもい」感情は募るのです。
差し当たり今のところ質問がでたら、次のようにしか答えられません。 例えば、まず円や直線が、球面や平面の一部と考えることができることを説明します。次の授業までに大きさの違う２個の林檎と１枚の海苔を用意し、林檎、海苔、林檎の順に串に刺して、接する２球面と接平面の関係を作ります。その後に包丁で中心を通らないように海苔に垂直に林檎を切ってやれば、その切り口にS.Ｌ問題の影を見ることできることを生徒に説明できると思います。
あるいは、もっと抽象的に、
「それはね、交わってる２円を離していってごらん。交点が１つになったら接線になるだろう。さらに離すとその影が残像として残るんだよ。」
こう済ませてしまうかもしれません。
さて、次にS.Lの問題は、受験数学の存在と弊害にまで飛び火してしまいました。私自身は、受験数学の存在および弊害は起こりうる現象と思っています。誰がそれを作ったのかということは言及すべきこととは思いません。Matheduで意見を述べている人達ではないでしょう。だからこそ「作ったのは誰？」という投げかけなのでしょうから。作ったらしい当人が不在でこの議論は収拾するのでしょうか。
そこで、受験数学があったと仮定して、ではそれは誰に対してのものかというとその対象はやはり、slow runnerになるのです。彼らはmy pace であるが故に、準備のインターバルに限りある受験に対して、一般的に要求される理解まで到達できません。やむなく、考え深い彼らはその思考を端折る手段を選んでしまいます。そこに現象としての受験数学とその弊害が生まれるのではないかと思います。
Ｓ.Lの問題にしても、前述のように交点の存在は明らかであるか、設問の中で確認される訳ですから単純に２円を引いてもよいということになりますが、２円を引くことの抵抗感を、交わらない場合も大丈夫なんだよと「納得」させることで、その「不安を解消」してやるべきだと思うのです。そこのところが曖昧になると、ただ引いただけで「何も考えていない」テクニック偏重の弊害となるのではと私は思っています。
ところで、受験数学は、誰かの指導の仮定の中で「納得」することと「説得」することのバランスが崩れたときだと考えられます。納得は知恵、説得は知識的傾向の指導だと思うのですが、どうでしょう。この両者は数学の理解(指導の結果としての)にはどちらも必要不可欠のものだと思いますが、受験へのインターバルの短さは、残念ながら生徒を説得してしまう圧力となっているのです。Ｓ.L問題の②の考察は、２球の交わりを使って説明していますが、現実問題として、２球の交わりがどんな図形になるか、イメージできない生徒の何と多いことでしょう。そこのところは生徒のイメージはどうでもよく、円なんだよと説得してしまうことの恐ろしさは誰でももっているのでしょうが、受験の圧力は説得することを選択させてしまうのです。
以上、結果として私の感想は、自身の教育論の展開となってしまいました。私はＳ.Ｌ問題においては数学的な解釈は教師の側で把握していれば十分であると思います。それをどう生徒に説明するかはオブラートで包んでやった方が生徒にとっては理解(納得)できるのではないでしょうか。
あとがきで、「きもい」感情は時が解決するだろうと書いているのですが、やっぱり解決するのは人なのでしょう。多分、私のこれからの教員生活の中でこの問題に一番納得のいく説明をしてくれるのは、slow runner なのではないかと思っています。
なお、前述の2球の交わりに関して指導の一事例として、＜２球の交わりについてのある授業風景＞なるレポートを用意しました。バーチャル・コンファレス上のバーチャル・レッスン(仮想授業)とでもなるのでしょうか。できれば、この授業風景に関するご意見をお寄せ下さい。私自身のコメントは、既に書いてあったのですが、敢えて本文からは削除しました。私の反省と皆さんの意見はどうオーバーラップするか、あるいは平行線となるか興味あることだと思っています。
＜あとがき＞
インターネットに無縁だった私は、いまインターネットに興味をもっています。