![]() 巒揰偺帇揰傪曄偊偰
巒揰偺帇揰傪曄偊偰
| 亂栤戣亃嶰妏宍俙俛俠偵偍偄偰丄俙俛傪侾丗俀偺斾偵撪暘偡傞揰傪俢丄俙俠偺拞揰傪俤偲偟丄慄暘俠俢偲慄暘俛俤偺岎揰傪俹偲偡傞丅俠俹:俹俢傪媮傔傛丅 |
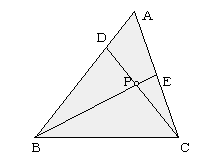 丂儊僱儔僂僗宆偺栤戣傪儀僋僩儖傪巊偭偰夝偔応崌丄巒揰偺愝掕偑廳梫側億僀儞僩偲側傞丅
丂儊僱儔僂僗宆偺栤戣傪儀僋僩儖傪巊偭偰夝偔応崌丄巒揰偺愝掕偑廳梫側億僀儞僩偲側傞丅
丂壖憐暯柺忋偺尨揰偵巒揰傪偲傞応崌偼愨懳嵗昗宯丄捀揰偺堦偮偵偲傞応崌偼憡懳嵗昗宯偱偺夝朄偲側傞偑丄偳偪傜傕巒揰傪掕揰偲傒偰偺峫嶡偱偁傞丅偙傟傜偺揰偼丄屌掕偝傟偨梫慺偱偁傞偐傜丄埵抲儀僋僩儖偺埖偄傕梕堈偱偁傝夝朄偺棳傟傕柍棟偑側偄丅偱偼丄偙傟埲奜偵巒揰傪愝掕偡傞偲偟偨傜偳偆偡傟偽偄偄偩傠偆偐丅椺偊偽丄慄暘偺暘揰偱偁傞俢丄俤傪峫偊傞側傜偽丄偙傟傜偺揰偼丄摦揰揑側怓崌偄偑嫮偄偐傜丄巒揰偲偟偰偺撻愼偼敄偄偲偄偆偙偲偵側傞丅傑偟偰傗丄媮揰偱偁傞揰俹偲傕側傞偲偄傢偢傕側偑偱偁傞偑丄幚偼偙傟丄怘傢偢寵偄偩偭偨傝傕偡傞丅屌掕奣擮偺妅傪幪偰偰嬛抐偺幚傪偐偠偭偰傒傞偲丄堄奜偲旤枴偟偐偭偨傝偡傞丅
丂偝偰丄偦偙偱偪傚偭偲偍悶暘偗傪偲巚偭偨師戞丅
夝乯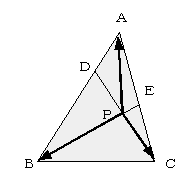 巒揰傪俹偲偡傞偲丄
巒揰傪俹偲偡傞偲丄
丂丂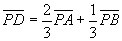 傛傝
傛傝 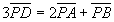 乧乧嘆
乧乧嘆
丂丂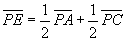 傛傝
傛傝 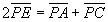 乧乧嘇
乧乧嘇
嘆亅俀亊嘇傪寁嶼偟偰丂乮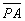 傪徚嫀乯
傪徚嫀乯
丂丂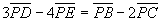
丂丂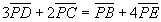
丂偙偙偱丄揰俹偑丄慄暘俠俢忋丄慄暘俛俤忋偺揰偱偁傞偙偲傪峫偊傞偲丄
丂丂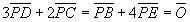 乧乧(仏) 偱偁傞丅
乧乧(仏) 偱偁傞丅
丂傛偭偰丄 丂丂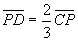 丄
丄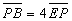
丂偙傟傛傝丄
丂丂俠俹丗俹俢亖俁丗俀
丂丂俛俹丗俹俤亖係丗侾
傪摼傞丅
丂偝偰丄偙偺夝朄偱偼丄儀僋僩儖偺堦師撈棫惈偼丄娫愙揑偵偟偐娭梌偟側偄丅(仏)偺幃偺嵍曈偼丄俁揰俹丆俢丆俠偑侾捈慄忋偵偁傞偙偲偐傜捈慄俠俢忋偺摦揰偱偁傞揰俹侾偺埵抲儀僋僩儖傪昞偟丄摨條偵丄塃曈偼捈慄俛俤忋偺埵抲儀僋僩儖俹俀傪昞偟偰偄傞丅偦偟偰椉曈偑摍偟偄偙偲偐傜丄俀揰俹侾丆俹俀偼俀捈慄偺嫟揰偱偁傞揰俹偵堦抳偡傞偺偱偁傞丅
丂偙偺傛偆偵丄媮揰俹傪巒揰偲峫偊傟偽丄揰俹偺埵抲儀僋僩儖偼丄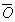 偲側傞傢偗偱偁傞偐傜丄揰俹偑慄暘偺拞怱乮暯嬒乯偵側傞傛偆偵慄暘偺斾傪攝偡傟偽傛偄偙偲偵側傞丅偦偙偱丄偙偺偙偲傪棙梡偟偰師偵暘揰偵偮偄偰峫偊偰傒傛偆丅
偲側傞傢偗偱偁傞偐傜丄揰俹偑慄暘偺拞怱乮暯嬒乯偵側傞傛偆偵慄暘偺斾傪攝偡傟偽傛偄偙偲偵側傞丅偦偙偱丄偙偺偙偲傪棙梡偟偰師偵暘揰偵偮偄偰峫偊偰傒傛偆丅