![]() 支点としての始点
支点としての始点
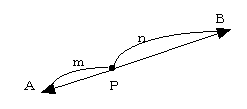 線分ABをm:nに分ける点Pは、点Pを始点とみると、
線分ABをm:nに分ける点Pは、点Pを始点とみると、
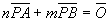 ……(*)
……(*)
を満たすのは明らかである(右図参考、外分点についても同様に考える)。
さらにこの始点をOに変えると、
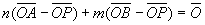
よって、
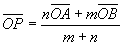
となる。
ここで(*)の式の点Pは、線分ABの中心であり、これは端点A,Bに重みをつけたときのバランス(加重平均)をとる点とみることもできる。特に、ベクトルを物理的な力とみなせば、点Pは、力のモーメントの支点(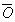 )と考えてよい。これから、(*)の式から線分比を読み取ることは簡単なことであり、したがい、上述のようにさらに分点の公式にまで変形する必要性はないのである。
)と考えてよい。これから、(*)の式から線分比を読み取ることは簡単なことであり、したがい、上述のようにさらに分点の公式にまで変形する必要性はないのである。
では、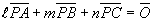 を満たす点Pはどんな中心になるのであろうか。支点を始点とみて求めてみよう。
を満たす点Pはどんな中心になるのであろうか。支点を始点とみて求めてみよう。
EX)三角形ABCにおいて、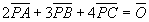 を満たす点Pを求めよ。 を満たす点Pを求めよ。 |
解)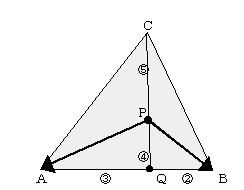
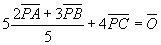
より、線分ABを3:2の比に内分する点をQとすると、
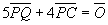

故に、点Pは、線分QCを4:5の比に内分する点である。
さて、これを一般化して、
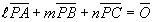
を、満たす点Pを求める。
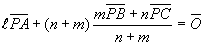
より、線分BCをn:m に分ける点をDとすると
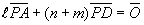
故に、点Pは、線分ADを(n+m):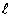 に分ける点である。
に分ける点である。
さらに、
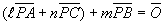
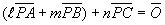
とみると、
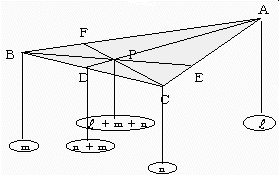
線分BCをn:mに分ける点をD、線分CAを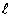 :nに分ける点をE、線分ABをm: :nに分ける点をE、線分ABをm: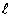 に分ける点をFとするとき、線分AD,BE,CFの交点が点P に分ける点をFとするとき、線分AD,BE,CFの交点が点P |
であることが分かる。
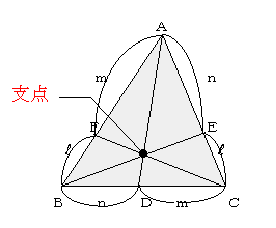 よって中心Pを支点とみれば、右図のようなモーメントのモデル図がつくられる。
よって中心Pを支点とみれば、右図のようなモーメントのモデル図がつくられる。
なお、一般に、
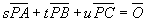 ,
,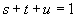 、s>0,t>0,u>0
、s>0,t>0,u>0
であるとき、s,t,uの組(s,t,u)を点Pの重心座標というが、この場合は、
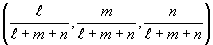
となる。特に、
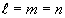 のとき、
のとき、
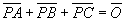 であり、重心座標は、三角形ABCの幾何学的重心
であり、重心座標は、三角形ABCの幾何学的重心![]() に一致する。
に一致する。
 Note)
Note)
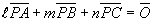 より、
より、
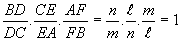
であるから、この式は幾何学的にみれば、点Pが三角形ABCの内部の点であるときには、チェバの定理を、外部の点であるときにはメネラウスの定理を表すことが分かる。
また、空間図形としてみれば、点Pは、同一直線上にない異なる3点A,B,Cが作る平面上の点であることを表す。
点Pは三角形ABCを含む平面上の点である。 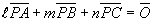 |
| EX) 四面体OABCにおいて、辺ABを1:2の比に内分する点をD、線分CDを3:5の比に内分する点をE、線分OEを1:3の比に内分する点をFとし、直線AFが平面OBCと交わる点をPとする。このとき、AP:FPを求めよ。 |
解)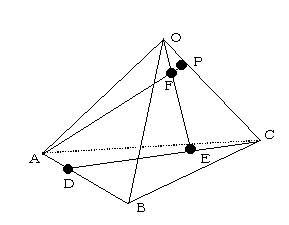 点Pを始点とする。
点Pを始点とする。
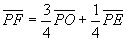
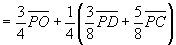
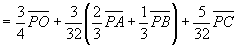
∴ 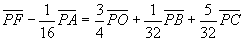 ………(*)
………(*)
ここで、点Pは、平面OBC上の点であるから、(*)の右辺=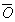 である。
である。
故に、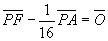 よって、AP:FP=16:1 である。
よって、AP:FP=16:1 である。
この問題の一般的な解法は、始点をOとして、直線のベクトル方程式を作り、パラメータの連立方程式に持ち込むのが常套手段であろう。だが、その場合、各分点の位置ベクトルは、D,E,F,Pの順に求められるから、計算の流れは分断されてしまうことになる。これを上述のように、始点を求点である点Pに設定すると、分点は逆に、F,E,Dの順に求まり、流れとしては実にスムースなのである。
点Pを始点として、分点を溯っていくと、最終的には点Pが、平面OBCと直線AFの交点であることに辿り着く。