面積としての支点の視点

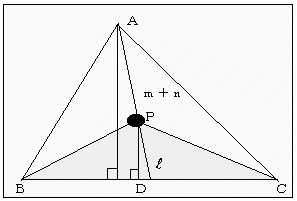
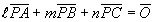　 を満たす点Ｐに対して、l，ｍ，ｎが図形的にどういった意味をもつのか面積との関係で調べてみよう。

　△ＡＢＣ＝Ｓ，△ＰＢＣ＝Ｓ_１とおく。

　頂点Ａ，点Ｐから対辺ＢＣに下ろした垂線の長さｈ，ｈ_１をそれぞれ三角形ＡＢＣ，三角形ＰＢＣの高さと考えれば、
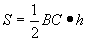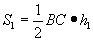　， であるから、
　　Ｓ：Ｓ_１＝ｈ：ｈ_１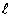＝(＋ｍ＋ｎ)：l

　同様に、△ＰＣＡ＝Ｓ_２，△ＰＡＢ＝Ｓ_３とすると、
　　Ｓ：Ｓ_２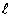＝(＋ｍ＋ｎ)：ｍ
　　Ｓ：Ｓ_３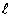＝(＋ｍ＋ｎ)：ｎ

　よって Ｓ_１：Ｓ_２：Ｓ_３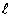＝：ｍ：ｎ となる。

　これから、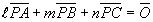 の係数は、三角形ＡＢＣの内部の点Ｐと頂点を結ぶ線分によって分割してできる３つの三角形（△ＰＢＣ，△ＰＣＡ，△ＰＡＢ）の面積比を表している。

　たとえば、点Ｐが三角形の重心であれば、 Ｓ_１＝Ｓ_２＝Ｓ_３ であるから
　　
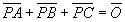
である。また点Ｐが、三角形ＡＢＣの内心であれば、Ｓ_１：Ｓ_２：Ｓ_３＝ａ：ｂ：ｃ より、
　　
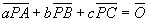
となる。

　このように、点Ｐは、三角形の面積（質量）のバランスをとる点（質量中心）となるわけである。

Ｎｏｔｅ）

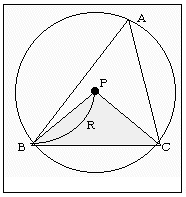
　点Ｐが三角形ＡＢＣの外心の場合は次のように求める。

　△ＰＢＣ
　　＝

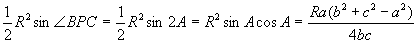
　△ＰＣＡ，△ＰＡＢについても同様であるから、
　　△ＰＢＣ：△ＰＣＡ：△ＰＡＢ
　　　　＝
　　　　＝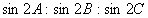