![]() 四点で作られる空間内の支点
四点で作られる空間内の支点
EX)正四面体ABCDの内部の点Pが、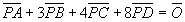 を満たすとき、点Pの位置を求めよ。 を満たすとき、点Pの位置を求めよ。 |
 解)
解)
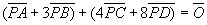
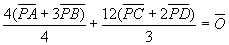
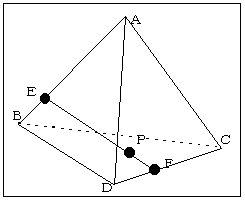
線分ABを3:1の比に内分する点をE,線分CDを 2:1の比に内分する点をFとすると、
![]()
∴ 点Pは、線分EFを、3:1の比に内分する点である。
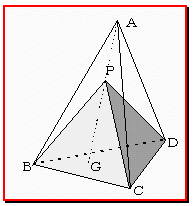
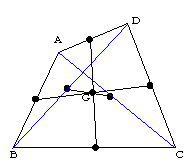 同一平面上にない4点(条件が曖昧であるが)により、ベクトル方程式としての空間が定まるが、4点A,B,C,Dを頂点とする四面体の内部に点Pをとるとき、
同一平面上にない4点(条件が曖昧であるが)により、ベクトル方程式としての空間が定まるが、4点A,B,C,Dを頂点とする四面体の内部に点Pをとるとき、
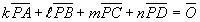
は何を意味するであろうか。上述のEX)のように考えると、
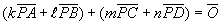
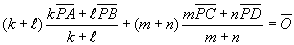
より、線分ABを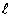 :kの比に内分する点をE,線分CDをn:mの比に内分する点をFとするとき、線分EFを、(m+n):(k+
:kの比に内分する点をE,線分CDをn:mの比に内分する点をFとするとき、線分EFを、(m+n):(k+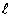 )の比に内分する点がPである。特に、
)の比に内分する点がPである。特に、
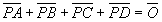 (k=
(k=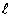 =m=n)
=m=n)
のとき、点Pは、辺AB,CDの中点を結ぶ線分の中点であり、これが四面体ABCDの重心となる(頂点を共有しない四面体の2辺の中点を結ぶ線分は1点で交わることも分かる)。
 さらに、k,
さらに、k,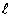 ,m,nを図形的に解釈してみよう。
,m,nを図形的に解釈してみよう。
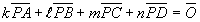 より、
より、
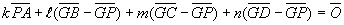
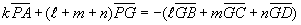
ここで、点Gを三角形BCDを含む平面上の点とすると、
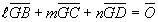 である。
である。
∴ 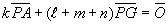
よって、点Pは線分AGを、(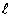 +m+n):k の比に内分する点である。
+m+n):k の比に内分する点である。
これから、四面体ABCDの体積をV,四面体PBCDの体積をV1とすると、
V:V1=(k+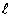 +m+n):k
+m+n):k
となる。
同様に、四面体PCDA,PDAB,PABCの体積をそれぞれV2,V3,V4とすると、
V:V1:V2:V3:V4=(k+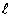 +m+n):k:
+m+n):k: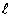 :m:n
:m:n
である。
以上より、点Pは、四面体ABCDの体積のバランスをとる点(質量中心)となる。
また、四面体の重心は、
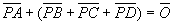
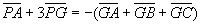
とみれば、三角形BCDの重心Gに対して、線分AGを3:1の比に内分する点である。